ミクロ経済学では、価格を企業が自由に決められる不完全競争を押さえることが大切です。この記事では、ラーナーの独占度に関する公式を解説します。
ラーナーの独占度の問題を解くときは、不完全競争市場の利潤最大化の条件である「MC=MR」をキーワードに押さえてください。
公務員試験では、不完全競争市場の分野が問われるケースもあります。受験される予定の方は、絶対に内容を押さえてください。
ラーナーの独占度とは
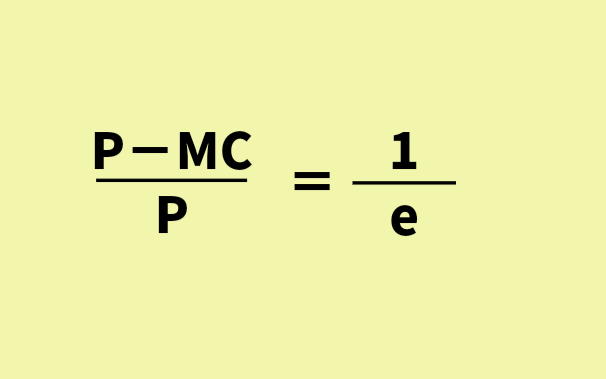
ラーナーの独占度とは、ある国の市場が完全市場の状態とどの程度乖離しているかを示した割合です。公式では、以下のように示されます。
完全市場は、需要と供給のみで価格が設定される社会を示します。ラーナーの独占度の公式を押さえるには、不完全市場を理解しなければなりません。
ここでは、不完全市場を簡単に説明した後、ラーナーの独占度の例題を取り上げましょう。
なお、完全競争市場については以下の記事を参考にしてください。
不完全競争市場(独占市場)
不完全競争市場とは、企業が価格を好きに決定できる市場のことです。独占市場とも呼ばれており、完全市場とともに重視されています。
日本では契約の自由が原則であるため、店頭に並べられている商品は販売者が自由に価格を設定できます。
無論、あまりにも高すぎる場合は無効とされるケースもありますが、必ずしも需給の一致で価格が決まるわけではありません。
皆さんが近くのラーメン屋で食事するときは、店長が独占して設定した価格に基づいて注文していると押さえてください。
ラーナーの独占度の求め方
ラーナーの独占度の求め方はです。
完全市場は、P=MCが成立する特徴を持っています。価格と限界効用が同じ値になるため、は1になるはずです。
一方で、不完全市場の場合はP=MCが成り立ちません。
そこでPがMCとどこまで離れているかを測るため、の式が用いられます。
なお、ラーナーの独占度は需要の価格弾力性(e)の逆数になります。式で表したものがこちらです。
需要の価格弾力性の逆数を取る理由は、数学的に解説できます。ただし、だいぶ複雑なので公務員試験なら覚えてしまった方が賢明です。
(※1)限界効用の解説はこちらを参考にしてください。
ラーナーの独占度の例題

(※画像はイメージです)
早速、ラーナーの独占度を使った例題にチャレンジしましょう。
とりあえず、の公式と「MC=MR」の関係だけは押さえてください。
正しい記述を答えるだけの問題であれば、この2つの知識だけで正答できる場合もあります。ここでは、計算問題がメインとなる例題を紹介します。
ラーナーの独占度で数量を計算
ラーナーの独占度を使い、数量(生産量)について求めてください。
X=12−P
ラーナーの独占度はです。
問題文からと式を作れます。
不完全市場はMC=MRになるため、各々の値を求めてください。面倒臭がらず、MCとMRを分けて計算した方が確実です。
MCの値について求める
式を計算し、MCの値について求めてください。
両辺にPをかけ
MRについて求める
次にMRを求めます。その前に需要曲線を変形し、P=12-Xと置きましょう。
TR(総収入)の計算式は
TR=X×P
つまり、X×(12-X)と書き換えられます。
するとTRはとなりました。
MRを求めるには微分が必要です。計算するとMR=となりました。
数量(X)を求めよう
最後にMR=MCの式を使い、数量(X)の答えを求めましょう。
まずは、MCの計算で求めたの「P」に「12−X」を代入してください。
すると、となるはずです。
まとめるとになりました。
MRの式と=(イコール)で結びつくため、
あとは落ち着いて計算してください。
したがって、数量は3です。
利潤最大化の理屈
不完全競争市場では、
MR(限界収入)=MC(限界費用)が利潤最大化を表すモデルでした。
例えば、パン屋さんが商売するためには原材料費や調理器具、電化製品などを購入しなければなりません。
商売道具を揃えるにも、一定のコストがかかってしまうわけです。
仮にMR>MCの場合、生産量を増加させたときは「収入の変化の割合」が高い状態を示しています。
いわば黒字になるため、企業は基本的にもっと多くの商品を販売しようと考えるはずです。
しかし、MC>MRになると今度はコストをかけすぎてしまいます。
損失を出さないギリギリのラインで生産活動を続けるポイントこそが、MR=MC(利潤最大化)です。
以下の記事でも詳しく紹介しているため、ぜひ参考にしてください。
需要の価格弾力性と逆数

(※画像はイメージです)
最後にオマケとして、ラーナーの独占度と需要の価格弾力性について深掘りします。先程、ラーナーの独占度は需要の価格弾力性と逆数になると解説しました。
その理屈を細かく書きますが、公務員試験レベルでは全くもって覚える必要はありません。
趣味として知りたい方のためにまとめます。参考程度に掲載しておくので、余裕かつ興味のある方はご覧ください。
MRを「全微分」で表す
まずは、MR(限界収入)の値を数式で表してみます。限界収入は総収入を全微分した値です。
TR(総収入)は価格×数量と簡単に求められます。ここでは価格をP、数量をQとします。PはP(Q)と置くことも可能です。
P(Q)は、価格がQによって決まることを示しています。
全微分=偏微分の合計
全微分をざっくりと解説すると、各文字の偏微分を組み合わせたものです。
例えば、とありました(f(x,y))。
Xを微分したときは、Yの微分は
となるはずです。
全微分は両者を合わせて求めます。
ちなみに、こちらは「積の微分公式」と呼ばれる方法です。
TRを全微分すると
簡単ではありますが、全微分の説明をしました。この要領でMRの式を作ってみましょう。
TR=P(Q)×Q。
P(Q)をQで微分したときの式は、MR=です…①
一方で、QをQで微分すれば「1」になるだけなので、先頭のP(Q)だけが残ります…②
①と②を合わせると、
以上でMR=と求まりました(P=P(Q))より。
需要の価格弾力性を分析
次に、需要の価格弾力性について分析しましょう。
公式を踏まえ、需要の価格弾力性が指す意味はコチラを参考にしてください。
数量を同じくQと置き、公式を簡単に書きます。
この計算式とラーナーの独占度を見比べれば、逆数の値を取る理屈が分かります。
ラーナーの独占度に代入
求めたMR=をラーナーの独占度に代入しましょう。
ラーナーの独占度は、が公式でした。
不完全競争市場が成立しているため、MCはMRに書き換えられます。
直接代入するとややこしくなるので、をP'と置き換えてください。
すると、と式が簡単になりました。
分子のPは0となり、とまとめられます。
変形させた式が、です。
ここで、需要の価格弾力性であると見比べてみましょう。
完全に逆数の値を取っていることが理解できると思います。
結果、ラーナーの独占度は需要の価格弾力性の逆数を取ることが分かりました。
は押さえておきましょう。
まとめ
今回は、ラーナーの独占度の例題の解き方を解説しました。公務員試験では、文字式を使ったもう少し複雑な問題が出てくるでしょう。
基本的な公式のを押さえてください。さらに、不完全競争市場の利潤最大化を示すMR=MCも問題を解くカギとなります。
TR(総収入)の求め方やMR(限界収入)の求め方もあわせて押さえましょう。