小学校まで習っていた算数が、中学校からは数学と名前が変わります。皆さんの中にも、なぜ名称が急に変わるのかが分からない方もいるでしょう。
この記事では、算数と数学の違いについてわかりやすく解説します。学生のみならず、中学生の子どもがいる保護者や塾講師されている方も参考にしてみてください。
算数及び数学の違い
中学校に進学して、算数の名前が数学になっても気にしたことがない方がほとんどでしょう。しかし算数と数学では、意味が全くもって違います。
算数の意味とは
算数は、日常生活に出てくる数字だけを使って計算する勉強です。
中学生になった皆さんは、ここで小学校の算数を思い出してみてください。「π」や「Y」といった文字式は使わなかったはずです。円も「3.14」で計算したでしょう。
また中学校3年生からは、「√(ルート)」を使った問題も出てきます。こちらも日常生活で用いる数字ではないので、算数には出題されません。
なお算数で用いるのは「0(ゼロ)〜自然数」の範囲のみです。負の数は使われないため、「1−3」という問題は「計算できません」が答えとなります。
数学の意味とは
一方で数学は、日常では使わない数字や文字も使いながら答えを出す科目です。
先ほど説明したように、「√(ルート)」や「π」といった文字式が数学から使われるようになります。
小学校では算数、中学校では数学を習うため、数学の方が難しいと考える人も多いでしょう。しかし中学受験に使われる算数は、数学を超えるほど難しい問題が出されます。
算数・数学の問題

画像がこのようにあります。条件に従いながら『半円の面積』を求めてください。ただし、算数の問題なので三平方の定理を使うことはできません。
算数を使った求め方

先ほど出題した問題の答えと解説を書いていきます。
まずは、この三角形が「直角二等辺三角形」になることを押さえましょう。その理由を含めて解き方を説明します。
補助線を引く
算数と数学の両方にいえますが、図形の問題では補助線を引くことを意識しないといけません。補助線は、答えを出すために自分で引く線です。
算数や数学は、この補助線を上手く引けるかが問題を解くカギとなります。「補助線を制する者は図形の問題を制する」といえます。
この問題では、辺ABに対して垂直となるような線を引きましょう。
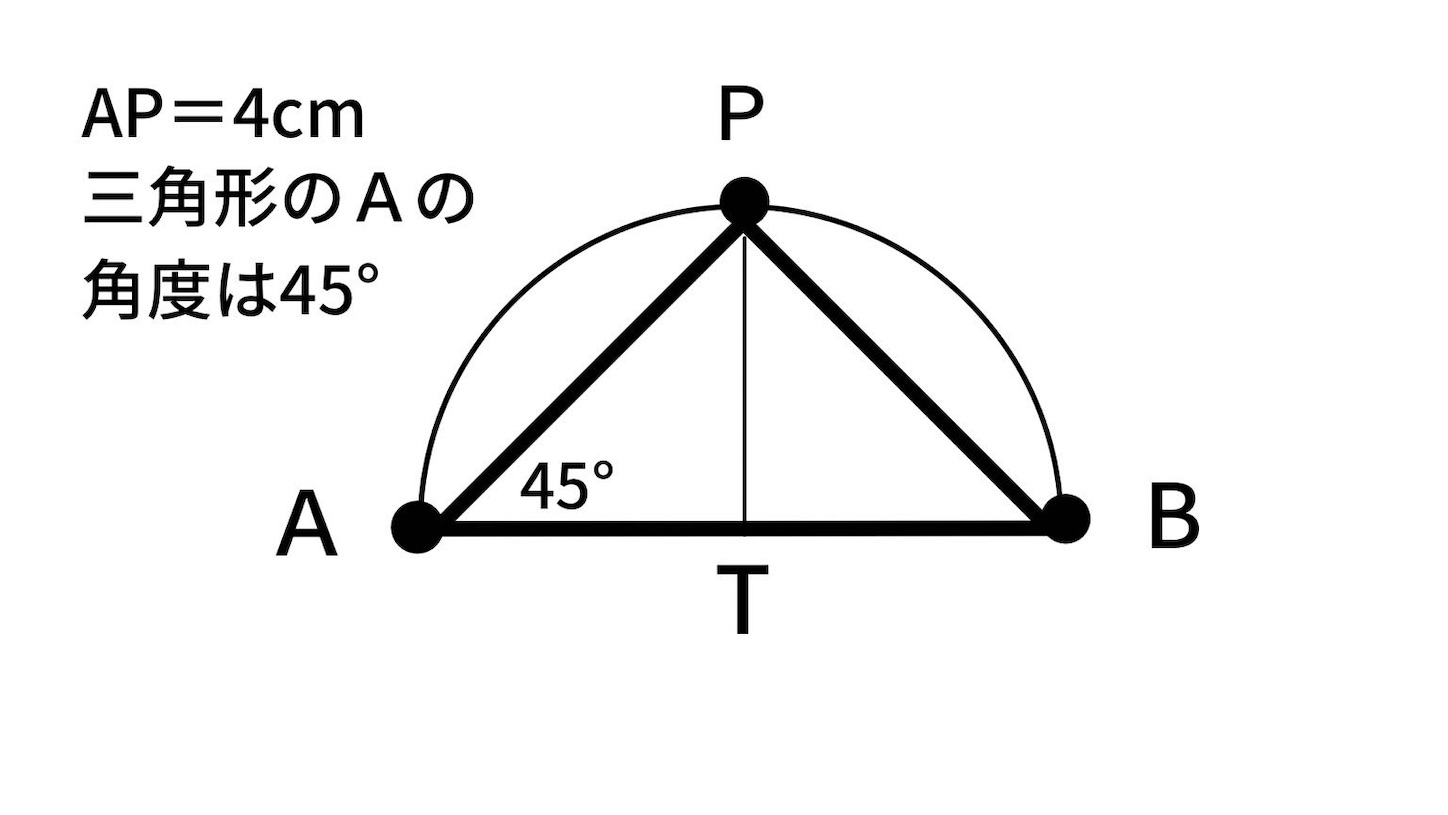
2つの二等辺三角形ができる
図で示したTは、辺ABの中心に来るのがわかります。辺ABは半円の直径と同じなので、このTは円の中心となっているのもポイントです。
点Tを軸にした「辺TA、辺TB、辺TP」は全て円の半径となりますよね。つまり、これらの辺は同じ長さです。
三角形APTや三角形BPTといった2つの直角二等辺三角形ができました。

正方形にして三角形APTの面積を求める
直角二等辺三角形を2つ作れたら、あとは半円の面積を求めるだけです。
辺APの長さは4cmとわかっていますが、これは中心を通っていないので円の半径ではありません。
三平方の定理が使えないため、計算できないのではと疑問に感じた方もいるでしょう。しかし底辺と高さが等しい直角二等辺三角形は、お互いの斜辺を合わせると正方形になります。

正方形の求め方は「たて×よこ」の他にも、対角線×対角線÷2という求め方があります。
正方形は対角線も長さが同じになるので「4×4÷2」で計算できます。したがって正方形の面積は8㎠です。
直角二等辺三角形の面積は正方形を半分に分ければよいので、三角形APTの面積は4㎠であると求められました。
半円の面積を求める

辺の長さだけ見ても、辺ATと辺PTの長さはわかりません。ただし三角形APTの面積が、4㎠になることさえわかれば、底辺×高さ÷2=4㎠の関係式が成り立ちます。。
今回の直角二等辺三角形は、以下の特徴を持っています。
- 底辺と高さの長さが同じ
- いずれも円の半径である
円を求める計算式は「半径×半径×3.14」ですが、今回は半円なので「半径×半径×3.14÷2」に直さなければなりません。
「半径×半径」は「底辺×高さ」と等しくなります。「底辺×高さ÷2=4」の式に当てはめれば、半径×半径の値は8となるはずです。
以上から半円の式に当てはめてみると
「8×3.14÷2=12.56㎠」なり、半円の面積が求まりました。
なお小数点を間に挟む場合、「8÷2」として先に整数から計算すると簡単です。
数学を使った求め方

数学をある程度習った方であれば、この問題は三平方の定理や円周の定理を使えば簡単に求められます。
鋭角がそれぞれ45°となる直角二等辺三角形の場合は、辺APと辺ABの長さの比率が「1:√2」になります。あとは辺ABの長さを比で求めるだけです。
1:√2=4:x
「x=4√2」になりました!
つまり辺ABの長さは4√2となり、半円の直径の長さと同じになります。。
後は、半円の面積を求めると
2√2×2√2×π÷2=4π
π=3.14と仮定すれば「4×3.14」で12.56㎠。先ほどと同じ答えを求めることができました。
算数や数学のコツについて
算数や数学といった計算を使う問題が苦手と感じる人は一定数いるでしょう。私自身も中学生や高校生のときは、あまり得意な科目ではありませんでした。
しかし大学生のとき、法律や経済学を勉強して数学の問題も昔よりはスラスラと解けるようになりました。
算数や数学は、順番を意識して覚えるのが問題を解くコツです。高校受験や大学受験では、習っていないところから出題されることはありません。
ただし、これまで習った範囲の単元を全部用いるので複雑に感じてしまうのです。
難関大学レベルになると、公式が本当に正しいかを証明する問題も出題されます。東大を目指しているのであれば、公式を丸暗記するだけでは足りません。
一方で苦手な数学を平均点は取れるレベルにする場合は、公式や解き方を覚えてしまうのも方法のひとつです。その際にも「なぜ、このような式ができるのか」を意識しながら覚えてください。