どーも、ヤマトノです。
今回はミクロ経済学の効用関数における限界効用の求め方を解説します。特に「u=xy」の式は重要であるため必ず押さえてください。
公務員試験においては、絶対に覚えるべき基礎的な計算式です。しっかりと内容を押さえ、軽々と問題を解けるように勉強しましょう。
なお、限界効用を求める際には以下のテキストをおすすめします。
まず、問題を解くときは「スー過去」を使用してみるといいでしょう。解説も詳しく記載されています。
ミクロ経済学の基礎を勉強したいときは、スー過去の下にあるテキストがおすすめです。練習問題も記載されており、初心者にもわかりやすく丁寧に解説されています。
※アフィリエイト広告を貼っている記事
効用関数とは?
まず、「効用関数」の言葉自体が聞き慣れないかと思います。
以前、ミクロ経済学には3つの視点があると解説しました。
- 消費者の視点
- 生産者の視点
- 市場全体の視点
詳しくは、こちらの記事を参考にしてください。
効用関数は、消費者の視点に立ったときの考え方です。
効用は「満足度」を指す
はじめに、効用とは何かを見ていきましょう。効用は「満足度」を指す言葉です。
例えば、お昼休みにコンビニで弁当を買ったとします。空腹な状態で弁当を買えれば、皆さんも満足度は上がるはずです。
ミクロ経済学では、「お金を払えば払うほど効用が上がる」と捉えます。手持ちのお金は気にせず、むしろ全て使い果たすケースが最も効用の高い状態です。
効用関数は右肩上がり
効用関数は、効用の変化をグラフにまとめたものです。
まずは、下記の図を参照してください(雑な仕上がりなのはごめんなさい)。
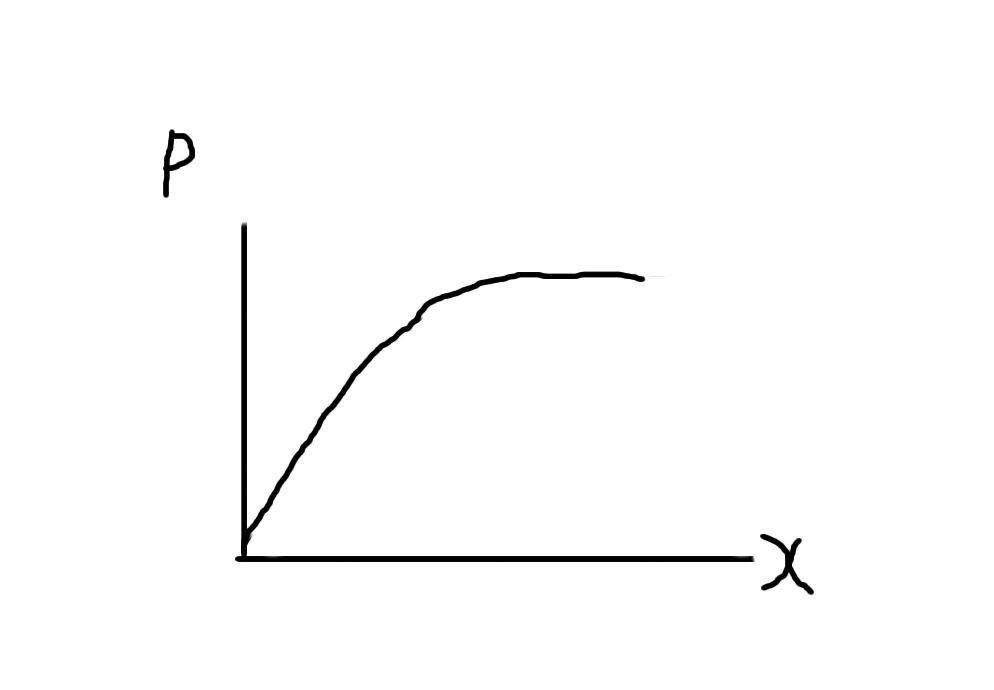
グラフははじめ勢いよく上がっているものの、数量が増えるに連れて上がり幅が小さくなっています。
こちらも先程のコンビニの例を出すと分かりやすいでしょう。空腹のとき、弁当を1個食べれば満足度が上がるだろうと説明しました。
それが2個に増えた場合、より多く食べられるため効用もさらに高まるはずです。
しかし、5個や10個と増えたらどうでしょうか?さすがに苦しくなり、買ったところで満足度は大して上がらないと思います。
ただ、ミクロ経済学では効用が下がるとは考えません。あくまで変わらず上がりつつも、その幅が小さくなっていくと捉えます。
限界効用の求め方
次に、効用関数における「限界効用の求め方」を解説します。
限界効用とは、数量が1増えたときに効用がどの程度上がったかを示す数値です。
弁当の例を出せば、1個から2個に上がるよりも5個から6個に上がる方が限界効用は小さくなります。特に解き方は大きく分けて2パターンあると覚えてください。
- u=xyの式のパターン
- 上記に該当しないパターン
では、これらの求め方を解説しましょう。
限界効用は「微分」が基礎
経済学で「限界」や「最大」の言葉が出たときは、ほぼ微分を使うと押さえてください。これを知っているだけでも、大半の問題が解けるようになります。
限界効用も例外ではなく、微分を使って求めます。まずは、以下の図にある問題を解いてみてください。

こちらは、最も基本的な形です。単純にuの式を微分すればいいため、Mu=6と求められます(Mu=限界効用)。数量が1であれば、限界効用の値は6です。
このような簡単なパターンは公務員試験には出題されません。基本は価格と結びつけて限界効用を求めます。専門的な内容について触れましょう。
u=xyは簡単な計算式
限界効用の求め方において、「u=xy」の形が出たらラッキー問題と思ってください。この計算式の解き方は非常に簡単です。こちらは、別名でコブ=ダグラス型と呼ばれます。
u=xyの形が来たら使用する公式は1つだけです。
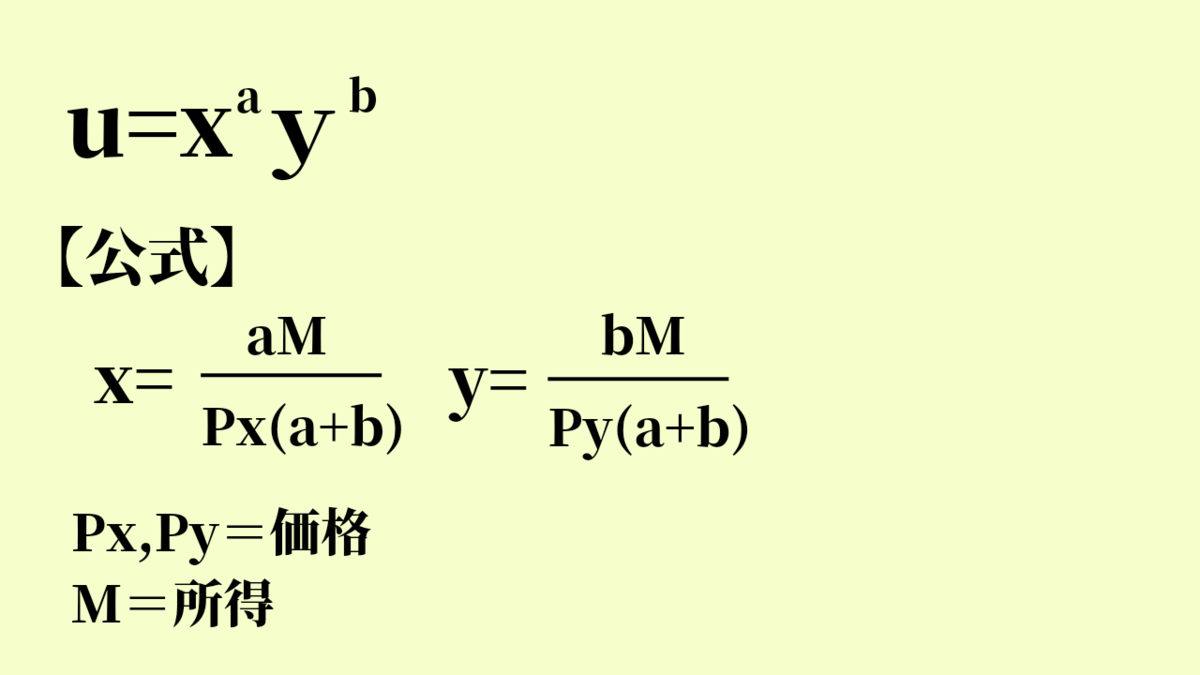
具体的な計算方法を解説しましょう。例えば、以下の式を用意しました。

この形では、指数がカギを握ります。解き方を画像とともに説明しているため、参考にしてみてください。
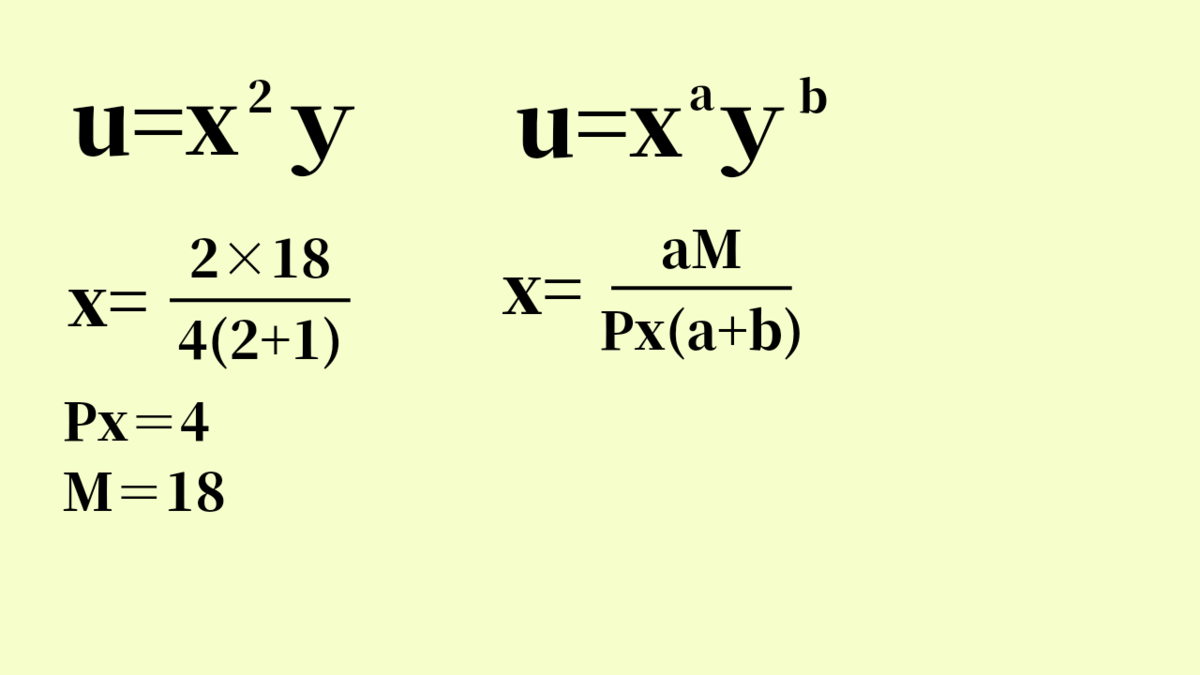
例題の式の指数はxが2でyが1です。分母はこれらの指数を合わせた数となります。つまり、3ですね。
さらに、Xの価格が4となっているので掛け算します。分母は12となりました。
一方で、分子はxの指数と所得を掛け算するだけです。所得は18となっているため、「18×2」で36になります。
約分すると限界効用時のxの最適消費量が3と求まりました。
形さえ覚えておけば当てはめるだけです。繰り返し問題を解きつつ、「u=xy」の形をマスターしましょう。
ちなみに、yの最適消費量も求められれば、xと掛け算するだけで全体の効用が求まります。
限界効用の計算の応用

すべての問題が「u=xy」で求められたら苦労はしません。しかし、限界効用にはコツコツと微分で計算しなければならない問題もあります。
また、練習として1つ例題を出しました。こちらを参考に求め方を押さえましょう。
まずは式の形に注目する
問題が出てきたら、まずは式の形に注目します。
例題は残念ながら項がたくさんあります(多項式)。ちなみに、項とは「+」や「-」で結ばれた数字の個数です。
このような形で出てきた場合、u=xyの簡単な式は使えません。文字式をひとつずつ微分をしてあげる必要があります。
加重限界効用均等で計算
次に加重限界効用均等の式を使って求めます。
公式は下図のとおりです。

xとyそれぞれで分子は限界効用、分母を価格にして=で結びます。
限界効用を求めるときは、微分を使います。

微分した結果、x財の場合はxyではxを消し、右の項のxは「1」です。上図にあるとおり、「x+1」がxを微分したときの式です。y財ではそのまま「y」になります。
価格は例題に書かれているため、それぞれを代入してください。すると、図の②のように「2(y+1)=3x」と式が作れました。
こちらは後ほど使うため、問題を解く際には余白にしっかりと数式を残しておきましょう。
予算制約線と連立方程式
続いて、例題の式を参考に予算制約線を作ります。
以下の関係性を押さえれば、式の作成は簡単です。
- 数量×価格=消費額
- 消費額=所得
財はxとyがあるため、これらを合わせると下記の式ができ上がります。

あとは、加重限界効用均等で求めたものとの連立方程式を求めましょう。連立方程式の解は、次のように導き出せるはずです。

【別解】予算制約線を代入する
先程は均等限界効用均等の式と予算制約線を連立方程式させてxとyの数値を求めました。
他にも、予算制約線を変形させて加重限界効用均等の式に代入する方法があります。「y=2x+10」のように全てが整数になれば変形させた方が賢明です。
ここで紹介した例題は、「y=」と直しても分数になるためこの方法は避けました。
問題の形式を確認し、どちらが望ましいかを判断してください。特に公務員試験は時間との勝負であるため、効率の良さが1番求められます。
限界効用を求める
このように、連立方程式でxとyの値を求めたら最後に「1単価あたりの限界効用」を求めます。ただし、単純にuの式に代入しないよう気をつけてください。
ここで求めたいものは、あくまで限界効用です。そのため、微分した状態で代入するよう手順を守りましょう。
まずはMuxの値を求めるため、「Mux=y+1」の式を使います。yを代入すれば「Mux=9」です。
次にMuyの値を出しましょう。「Muy=x」となり、「Muy=6」と出せれば問題ありません。
最後に、1単価あたりの限界効用を導き出します。方法としては、それぞれの限界効用を価格で割り算するだけです。
つまり、上述した「加重限界効用均等」の公式を使いましょう。

上図を計算すれば、MuxもMuyも「3」と求まりました。したがって、1単価あたりの限界効用は3です。
まとめ
今回は、効用関数での限界効用の求め方について解説しました。
まずは、経済学において「限界」の文字が出てきたら「微分」と押さえてください。次にu=xyの簡単なやり方を完璧にできるよう準備しましょう。
ただし、効用関数の形によってはu=xyで求められないケースもあります。加重限界効用均等と予算制約線の計算方法もできるようにした方が賢明です。
今後も公務員試験のミクロ経済学を勉強したい方は、僕のブログを登録してみてください。 加えて、計算ミスなどがありましたら教えていただきますと幸いです!
- 限界効用の基本は微分
- 「u=xy」の式かを確認
- 多項式は加重限界効用均等