皆さんは中学校の数学で正負の数を習った際に、なぜマイナス同士のかけ算が「+」になるのか疑問に感じたことはありませんか。
以前、とある学校の教頭先生とお話させていただいたところ、マイナス同士の計算を説明できない先生が多いと悲しんでいました。
ここでは基本に立ち返って、中学校1年生の数学に出てくる正負の数を解説します。現役の中学生だけではなく、保護者や塾講師もぜひ参考にしてみてください。
※アフィリエイト広告を貼っている記事
マイナスを使った計算問題

では、手始めにこれらの問題を解いていきましょう!
どれも中学校1年生で勉強する問題です。計算自体はそこまで難しくありませんが、「+」と「−」の符号を付け方で悩むかもしれません。
問題の解答と解説
上から順番に問題の解答を並べましょう。
- 6
- −25
- 16
まずマイナス同士のかけ算となる問1は、符号を「+(プラス)」にすることさえ忘れなければ単純な「3×2」の計算です。
問2の場合は、まず先に「5×5」の計算からする必要があります。そこで求めた解にマイナスの符号が付くため、最終的な値は-25です。この順番が間違いやすいので注意してくださいね。
一方で問3は、(-2)を4回かけ算する計算です。カッコのあとに指数があるパターンとカッコの中に指数があるパターン(もしくはカッコなし)で分けて覚えましょう。
マイナス同士のかけ算が「+」になる理由
最後にマイナス同士のかけ算が「+」になる理由をわかりやすく解説します。
私が説明するときに使うのは数直線です。数直線に人が歩く様子をイメージすれば、マイナス同士のかけ算も説明しやすいと思います。
「3×2」の考え方
マイナス同士のかけ算を説明する前に、プラス同士のかけ算がどういうものかを解説しましょう。
私の考え方を使う際には、以下の条件を押さえてください。
- かけられる数は「顔の向き」と「歩数」を指す
- かける数は「歩く向き(前後)」と「回数」を指す
つまり「3×2」はプラスの方向を向きながら3歩、前に向かって2回歩きます。
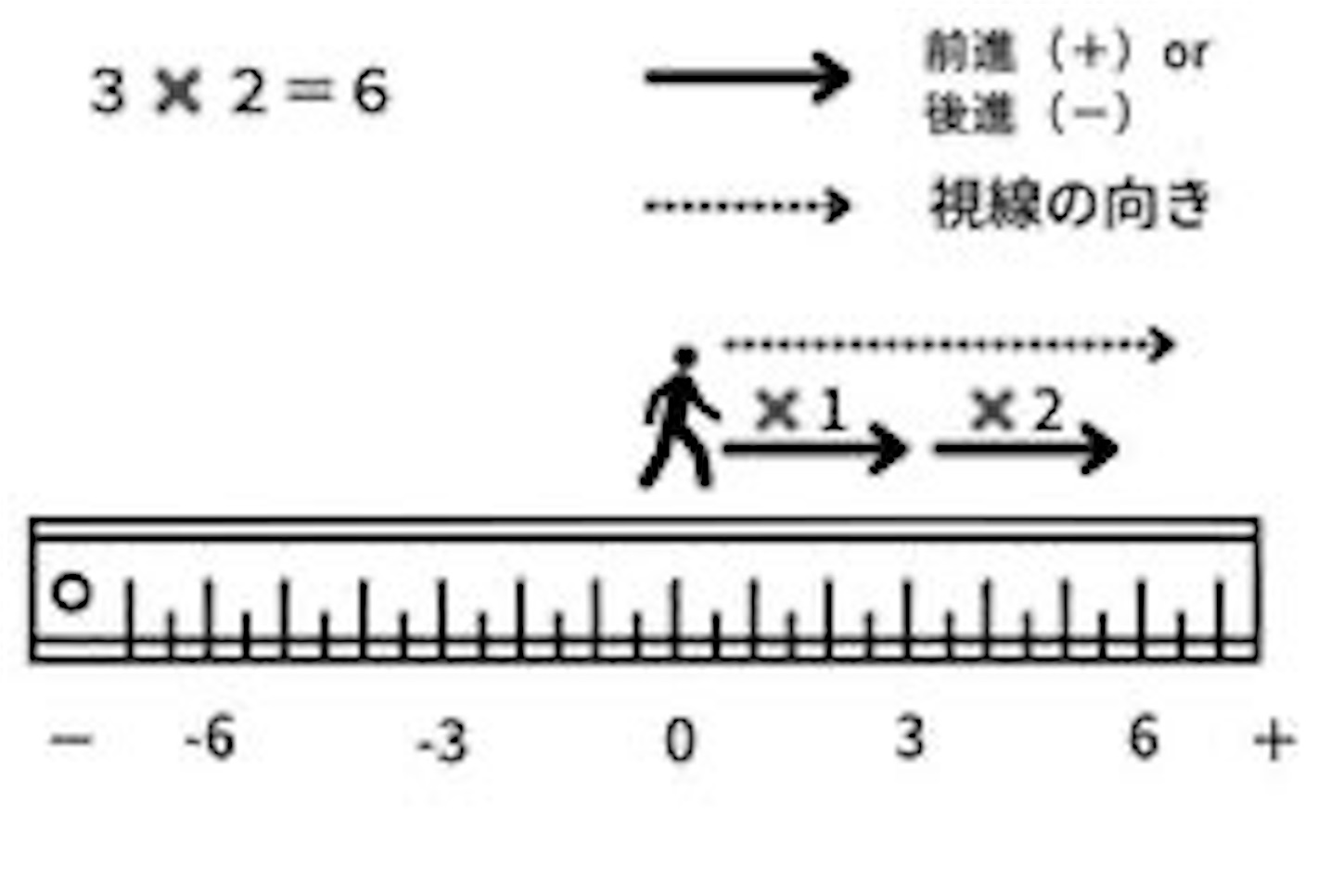
上記の数直線のように、3歩ずつ歩けば最終的に「+6」の地点に到着するでしょう。
-3×2や3×(-2)の考え方
次にかけられる数あるいはかける数のいずれかが、マイナスの符号が付いているパターンを解説します。答えは「-6」ですが、同じく数直線を使って考えてみましょう。
まず「-3×2」の場合は、条件が以下のようになります。
- マイナスの方を向き歩数は3歩
- 前に向かって2回進む
つまり下図のように進めばよいわけです。
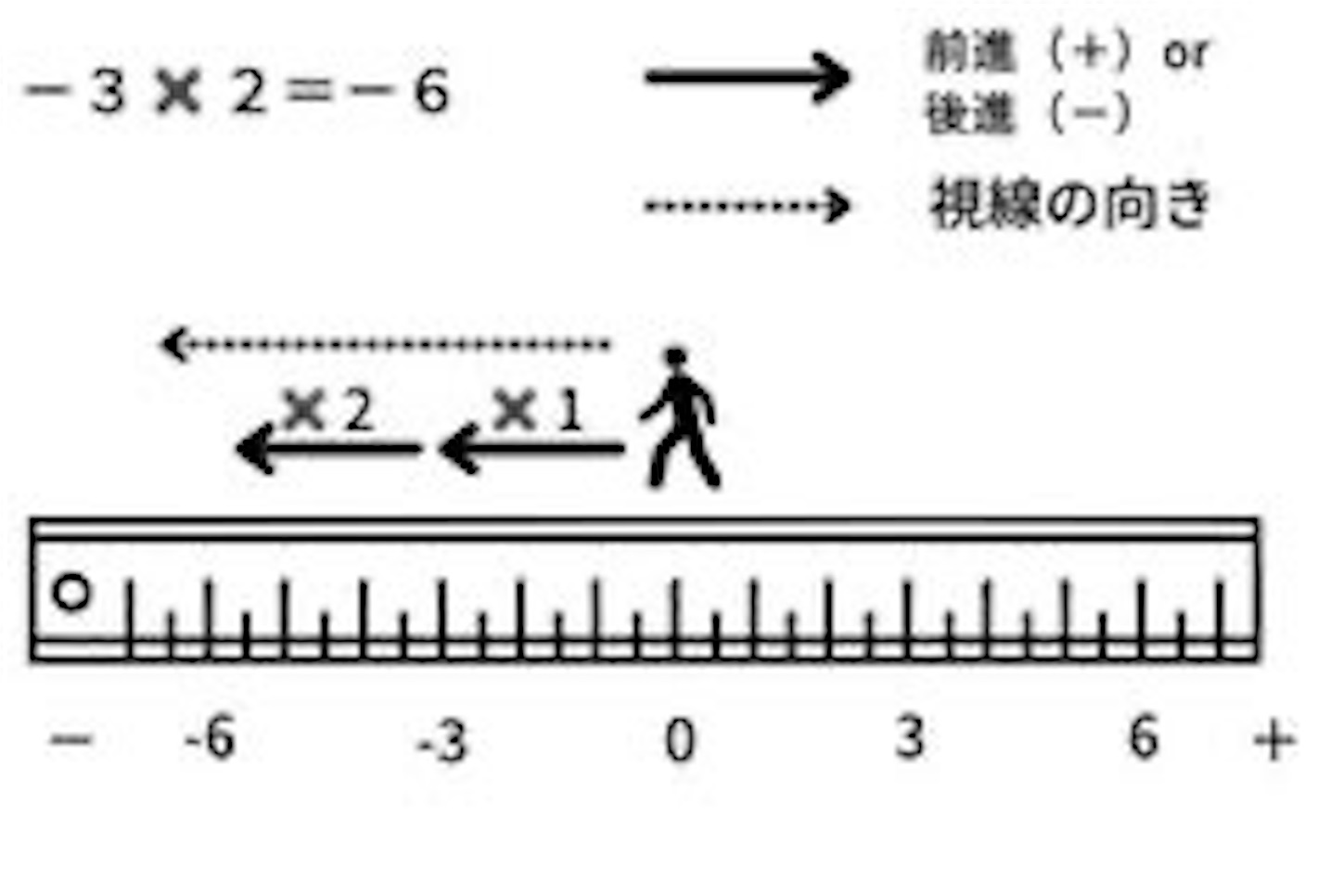
すると「-6」の地点に到着しました。
「3×(-2)」になるとプラスの方へ向いて3歩、バックする(後ろに歩く)形で2回進みます。
サザエさんのエンディングのように進ませると、同じく-6の位置にたどり着くはずです。
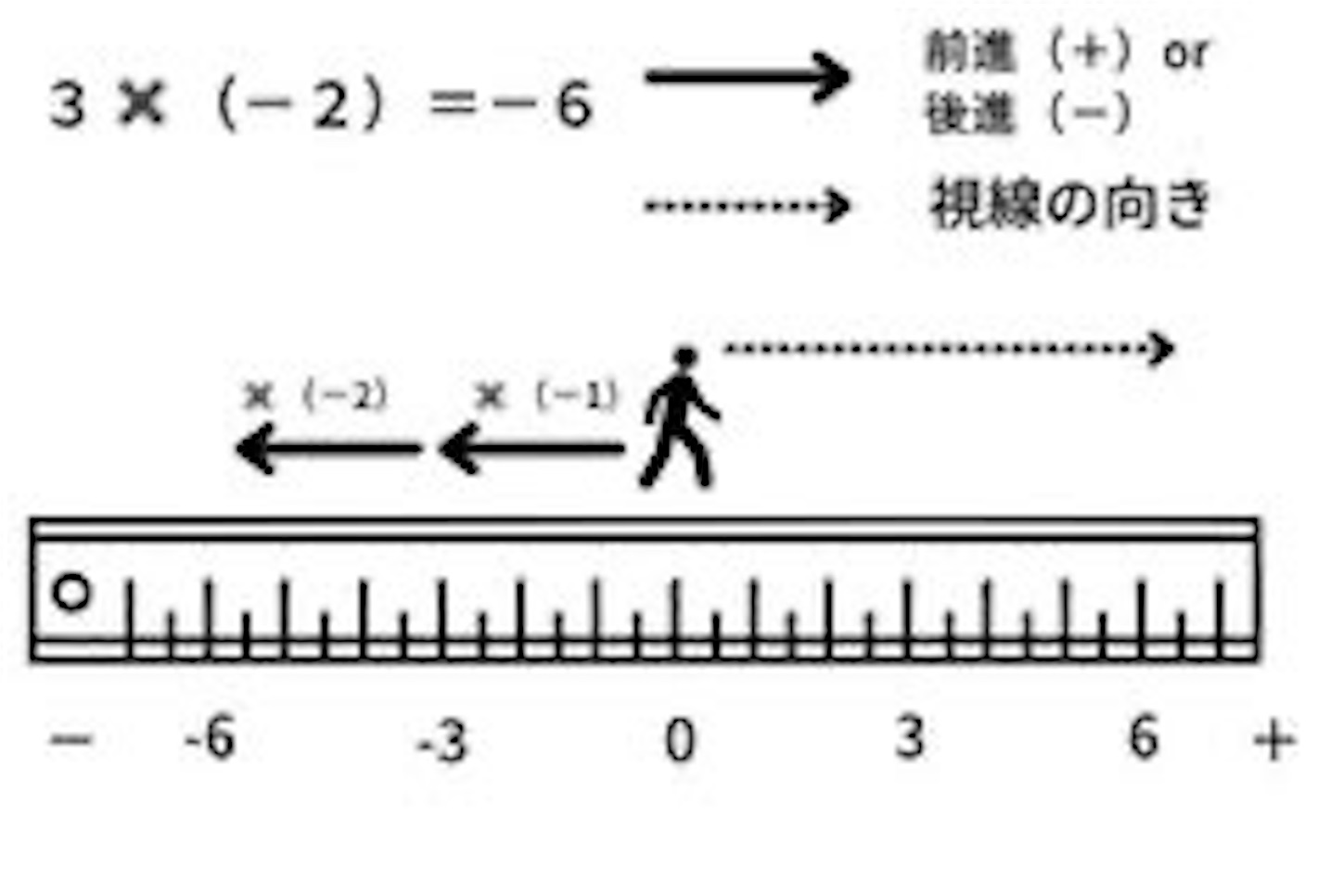
-3×(-2)の考え方
これまでのやり方を踏まえて、マイナス同士のかけ算を考えてみましょう。
かけられる数が「-3」であるため、マイナスの方を向き歩数は3歩となります。次にかける数が「-2」であることから、後ろ向きに2回進むと仮定してください。
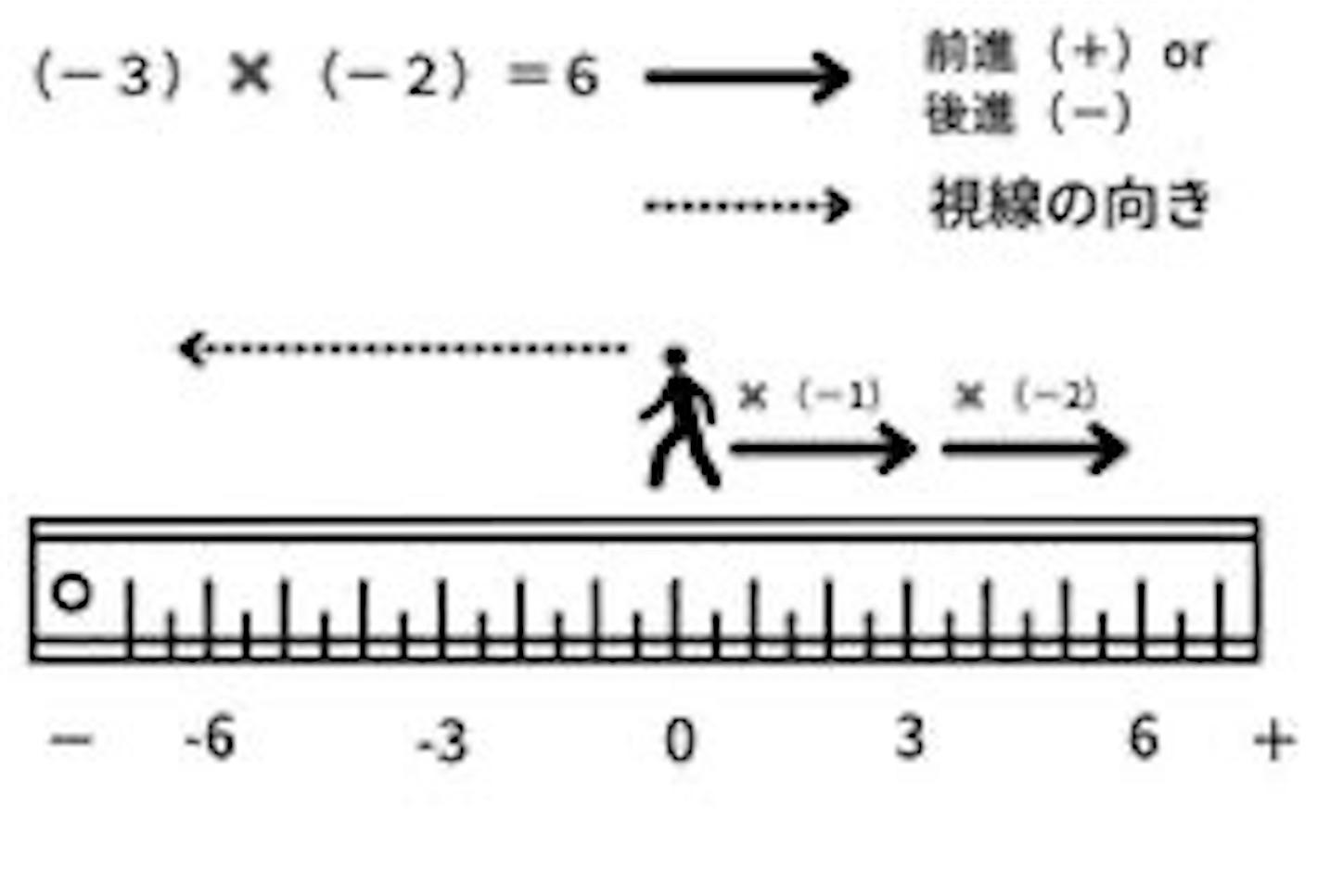
すると最終的にこの人物は「+6」の地点に到着しました。以上からマイナス同士をかけ算すると、解はプラスになるといえます。
「考えて」問題を解くのが大事
中学校や高校数学で重要なのは、なぜそう計算できるかを考えることです。
数学の問題を解くにあたって、わからないときは答えを見たほうが勉強の効率は良くなります。しかし何も考えずに解法を暗記しようとしても、なかなか記憶が定着しません。
何度も問題を解きながら、なるべく計算の理屈を理解できるようにしましょう。
中学校の数学の問題をどんどん解きたい方は、以下のような参考書を購入してみてください!