マクロ経済学のIS-LM分析では、主に財市場と貨幣市場の動きを分析しました。一方で、財市場と貨幣市場の分析を合わせた概念である総需要曲線も存在します。
この記事では、公務員試験受験者に向けて総需要曲線の求め方を解説します。AD-AS分析を含め、今後のマクロ経済学の内容にも繋がるので押さえてください。
総需要曲線の求め方
総需要曲線とは、財市場と貨幣市場の動きをセットで捉えるグラフのことです。英語ではAD(Aggregate Demand)と表現できます。
IS-LM曲線では、財市場と貨幣市場の変化から国民所得と利子率の関係を捉えました。しかし、実際の我々の生活には「物価」も大きな影響を与えます。
そもそも「総需要」を平たくいえば、国全体の需要の総和を指します。国民全員の需要を考慮するうえでは、物価は切っても切り離せません。
そこで国民所得と物価の関係も視野に入れたのが総需要曲線です。
総需要曲線の成り立ち
総需要曲線の成り立ちについて、IS-LM曲線も用いながら解説しましょう。
例えば、次のIS-LM曲線を見てください。
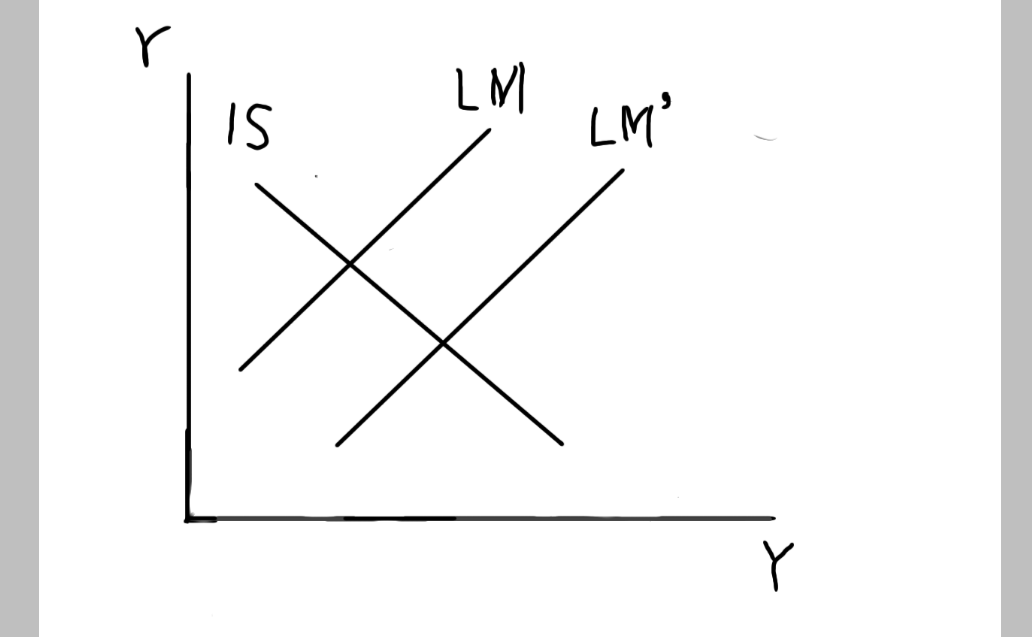
こちらの図では、LM曲線の方が金融緩和などの理由で右側にシフトしています。この場合、利子率も下がりつつ国民所得を伸ばしていることが分かります。
LM曲線の動きを捉えたうえで、総需要曲線の変化も見てみましょう。総需要曲線を描くときは、縦にP(物価)と横にY(所得)を置きます。
LM曲線が右側にシフトすると、大前提として国民所得は増加します。つまり、当該変化によって国民所得が伸びる様子を総需要曲線で描かなければなりません。
IS-LM曲線ともに影響を与えるので、総需要曲線は1本の線で表すのも条件です。これらの条件を踏まえると、以下のように変化を捉えられます。
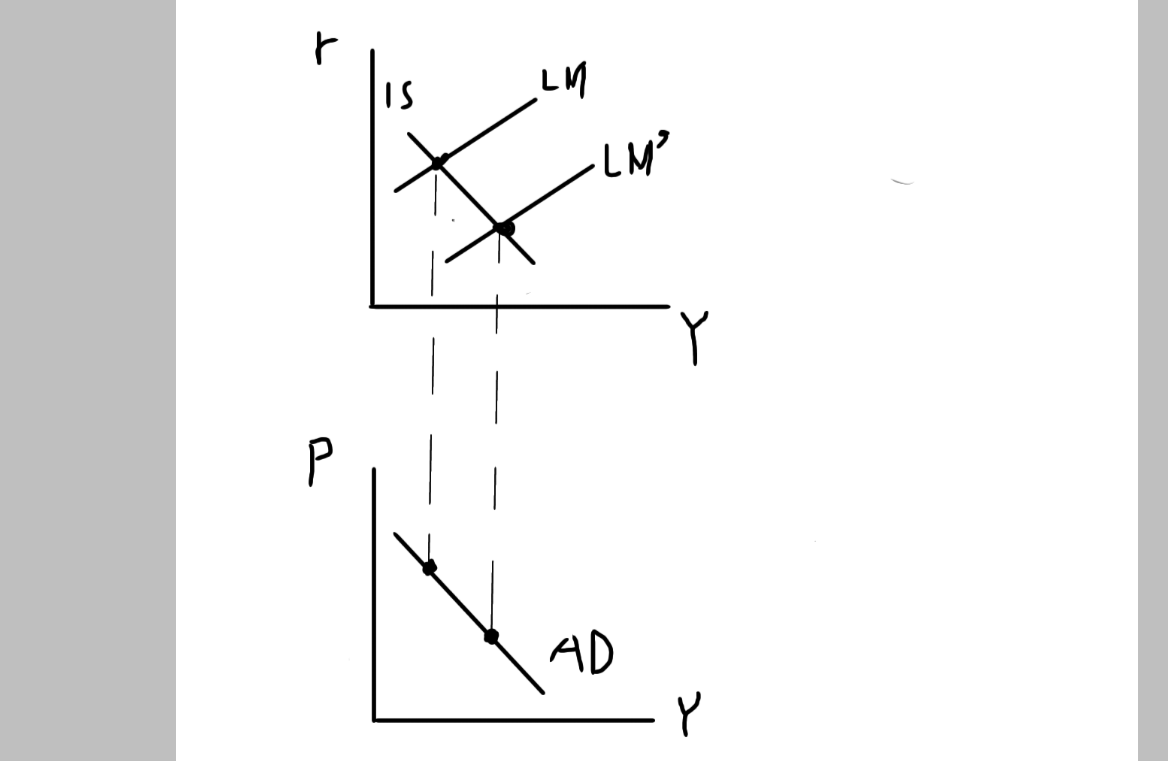
結果的に、総需要曲線は「右肩下がり」のグラフが描かれると覚えてください。
物価水準とLM曲線
続いて、物価と貨幣の関係について解説します。物価が上がると、店頭に売り出される商品の値段も相対的に上昇します。
市場の物価が上がる理由は、相対的に見て貨幣の価値が下がっているからです。その一因として、単純に貨幣供給量が増えすぎている可能性もあります。
そこで、一般的には金融引き締めによって流通する貨幣量を減らそうと国は試みます。この流れをマクロ経済学で表す際には、LM曲線を左側にシフトしなければなりません。
要するに、物価の上昇はLM曲線を左にシフトさせる要素の一つです。
反対に物価が下落すれば、LM曲線は右側に動きます。この特徴を総需要曲線で表すと次のようになります。
- 物価上昇は国民所得を下げる
- 物価下落は国民所得を上げる
こちらは、あくまで総需要曲線で見た場合の変化の特徴です。実際の経済では、物価の大幅な下落はデフレーションを招くので望ましくないと考えられています。
総需要曲線の動き
総需要曲線も、IS-LM曲線に合わせて動くのがポイントです。公務員試験でも、どのようにシフトするかを問う問題が出題されます。
IS-LM曲線シフト
まずは、IS曲線やLM曲線が右側へシフトした場合の状態を解説します。
右側のシフトは、それぞれ以下の変化を示している状態です。
- IS=財政拡大をしている
- LM=金融緩和をしている
そのため、どちらも国民所得を上げる作用があります。このようなシフトをした場合は、総需要曲線も同様に右側へ動くと押さえてください。
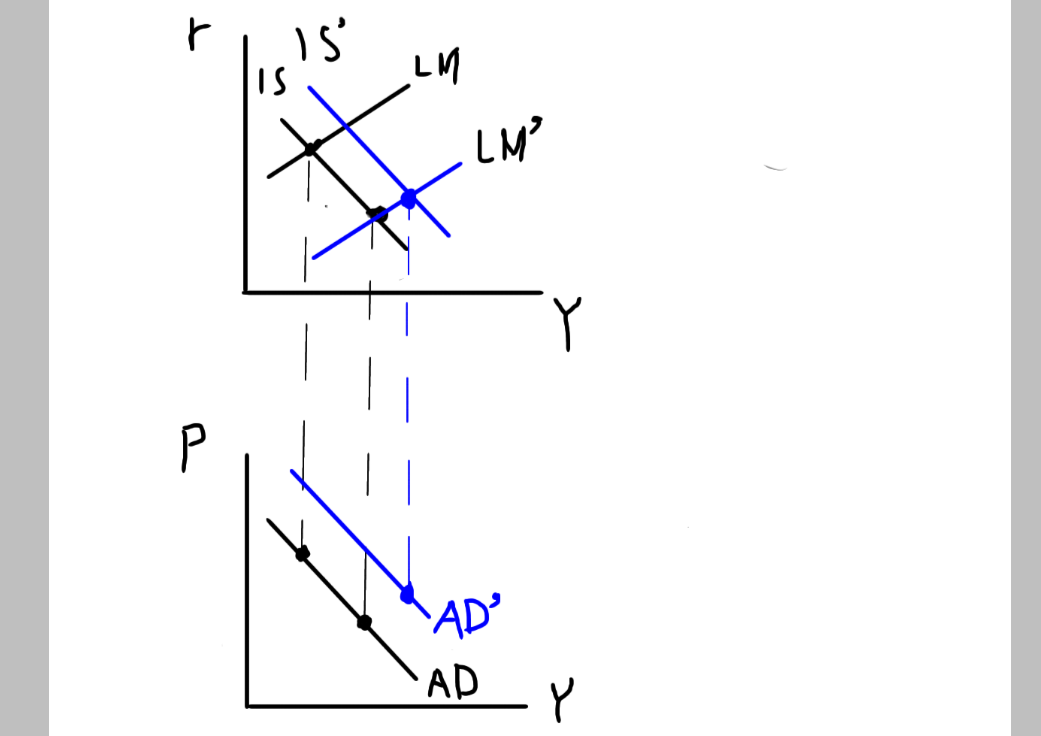
反対にIS曲線とLM曲線が左側へシフトした場合は、総需要曲線も左側に動きます。国民所得と連動すると押さえれば、この特徴も問題なく覚えられるはずです。
IS曲線が垂直・LM曲線が水平
IS曲線が垂直かつLM曲線が水平な場合は、総需要曲線は垂直になります。
IS曲線が垂直とは、投資の利子弾力性がゼロの状態のことです。LM曲線を移動させても、国民所得が変化しません。
要するに、物価をいくら操作したところで国民所得が増えない状態を示しています。結果的に総需要曲線は横軸(所得)に対して垂直となります。
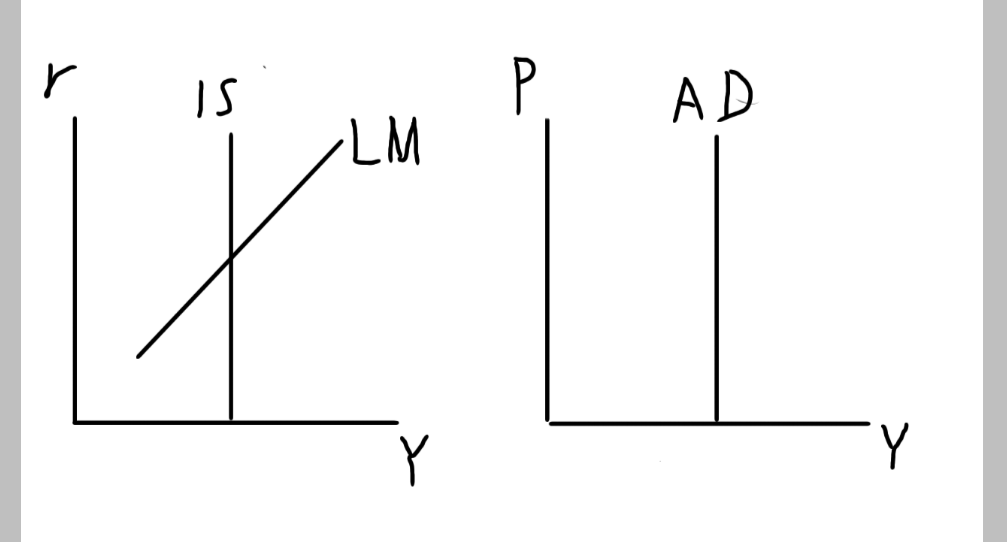
一方で、LM曲線が水平とは流動性の罠が生じている状態です。こちらも貨幣市場をコントロールしたところで、国民所得は変化しないのを示しています。したがって、総需要曲線は同じく垂直に描かれます。
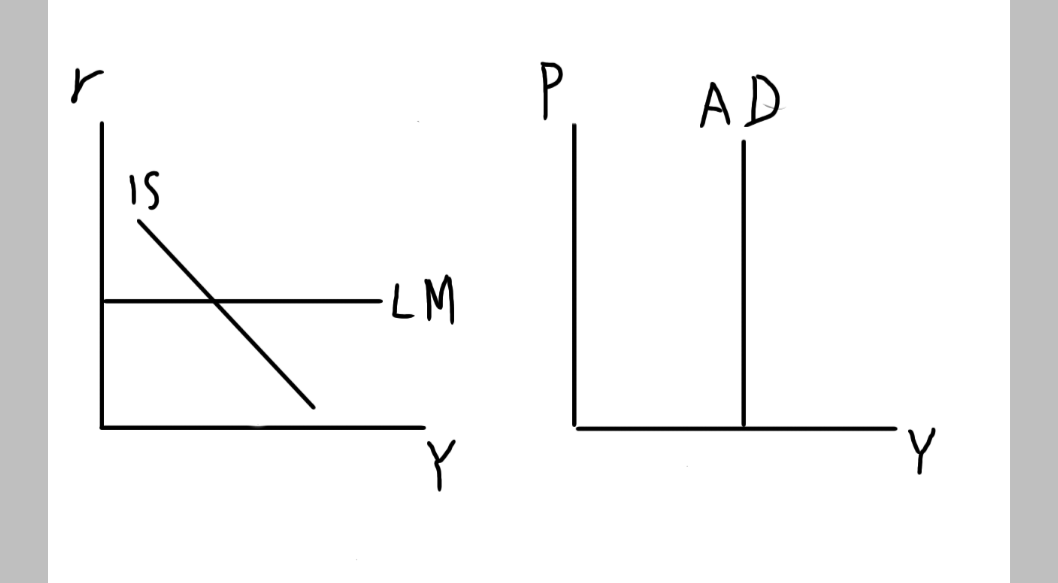
LM曲線をいくら動かしても、国民所得が変化しようがない場合に総需要曲線は垂直になると覚えましょう。
流動性の罠については、以下の記事でも解説しています。覚えていない方は、ぜひこちらも参考にしてみてください。
総需要曲線の計算

総需要曲線は、計算式を使った求め方も頻繁に出題されます。知識問題のみならず、計算問題も練習して上手く対応しなければなりません。ここでは、例題を出しながら解説しましょう。
総需要曲線の例題
例えば、ある国の経済が以下の条件で示されていたとします。
C=25+0.8Y
I=30−5r
G=35
L=Y−5r
M=480
この場合の総需要関数は次の①〜③のどれか
①
②
③
IS曲線の式をまとめる
まずは、マクロ経済学ではおなじみのY=C+I+Gの式を作ります。こちらの式は、財市場の状況を表しています。つまり、IS曲線を示していると捉えてください。
問題文の数字をそれぞれ代入すると、式は次のように作られるはずです。
Y=25+0.8Y+30−5r+35
数学の要領で各数字をまとめてみましょう。
0.2Y=−5r+90
Y=−25r+450
LM曲線の式をまとめる
続いて、LM曲線の式をまとめます。物価水準のPが邪魔に思えますが、我慢して計算に含めなければなりません。
=Lに代入すると、以下の式が完成されるはずです。
=Y−5r
Y=+5r
連立方程式を解く
IS曲線とLM曲線で求めた計算式を、連立方程式して総需要関数を導き出します。
- Y=−25r+450…①
- Y=
+5r…②
連立方程式を解くときは、とりあえずr(利子率)を消すことを意識しましょう。この場合は、②の式に「×5」をしてrの数字を揃えます。すると、以下のように求められるでしょう。
5Y=+25r…②
rの数字が揃ったら、①と②の式をまとめます。まとめた結果、式は次のようになりました。
6Y=+450
=6Y−450
P=
P=
したがって、正解は①になります。
総需要曲線のまとめ
今回は、総需要曲線の求め方について解説しました。総需要曲線は、財市場と貨幣市場の双方の動きを捉えているグラフです。ここでは、以下の特徴を押さえてください。
- 総需要曲線は右肩下がり
- IS・LM曲線が右に動くと総需要曲線も右にシフト
- IS・LM曲線が左に動くと総需要曲線も左にシフト
- IS曲線が垂直だと総需要曲線も垂直
- LM曲線が水平だと総需要曲線は垂直
また、総需要曲線は計算問題が出題されるケースもあります。計算自体は面倒なところもありますが、落ち着いて連立方程式を解くように心がけましょう。