どーも、ヤマトノです。
ミクロ経済学を勉強では、関数を読み解く力が求められます。
以前、関数のひとつである「生産関数」について解説しました。
この記事では、生産関数を作る上で基礎となる等量曲線と等費曲線を学びます。
等量曲線や等費用線は、資本と労働の関係性を知るときにも重要です。
それぞれのグラフの特徴とあわせ、技術的段階率の意味も解説しましょう。
等量曲線とは
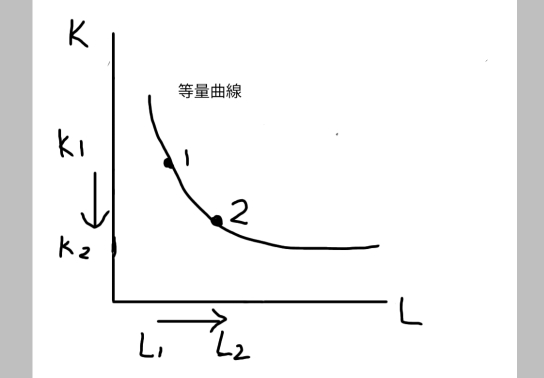
等量曲線とは、製品を生み出す際に必要となる資本(K)と労働(L)の組み合わせを示したグラフです。
グラフの構造は、無差別曲線と似ています。(無差別曲線については以下のリンクから)
企業が生産活動をするうえで、心がけるべきポイントがいかに費用を抑えられるかです。
費用を抑え、なおかつ売上を増加させれば利益が膨らみます。
生産活動で、特に費用がかかるのが資本と労働(人件費)です。
等量曲線では、どの程度の配分で両者を取り入れるかを分析します。
等量曲線のグラフの描き方と技術的限界代替率を紹介しましょう。
等量曲線は右下がりに描く
まずは、等量曲線の描き方について紹介します。描く際には、縦軸に資本(K)と横軸に労働(L)を置くのが基本です。
等量曲線は無差別曲線と性質が似ており、右下がりのグラフを示します。

つまり、資本と労働はお互いに負の相関を持つと押さえてください。
予算が同じであるとき、労働力を増やせば自ずと資本にかける分が少なくなるでしょう。
反対に機械の導入をどんどん促進すれば、労働者の数を増やす余裕もなくなります。
もし、両者ともに数を増やしたい場合は、予算そのものを増加させるしかありません。
予算を増加させたときのグラフは、右上の方向に移動します。
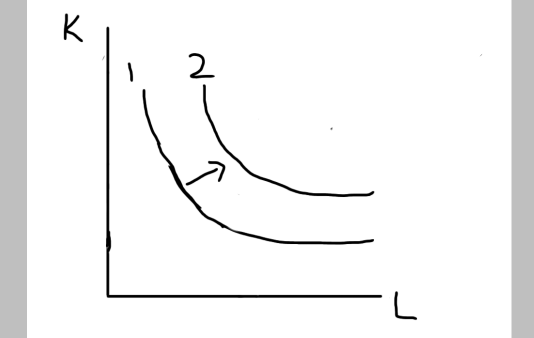
等量曲線を無数に描いたとしても、これらは接触しない点も押さえてください。
全て無差別曲線にも当てはまる考え方です。

無差別曲線を勉強すれば、大まかなルールは 分かるね!
技術的限界代替率との関係性
等量曲線を捉える際には、技術的限界代替率との関係性も押さえてください。
技術的限界代替率とは、等量曲線の変化の割合です。
式ではと示されます。
先程も触れたとおり、資本と労働には負の相関があります。
生産量を同じにする場合、労働力を上げるのであれば資本が下がるのが基本です。
この関係性を技術的限界代替率逓減の法則と呼びます。
限界生産力との関係
技術的限界代替率はと示されると説明しましたが、もう1つ重要な概念が限界生産力です。
限界生産力とは、生産要素(資本、労働)のいずれかを増やすときに得られる生産物の増加分を指します。
各生産要素の限界生産力は、以下のように表します。
- 資本…MPK
- 労働…MPL
例えば、労働力を⊿L単位増加させたとしましょう。
このときの限界生産力は⊿L・MPLです。労働力を上げると資本は⊿K分下がるため、⊿K・MPKが同時に減少します。
お互いに変化量は同じであるため、以下の関係性が成り立ちます。
⊿L・MPL=⊿K・MPK
式を変形したものがこちらです。
技術限界代替率が限界生産力の比と等しくなることを示しています。
等費用線とは
等費用線とは、企業が生産要素にかかる費用を示したグラフのことです。
記号を使って解説するため、下記の条件を押さえてください。
- C…費用
- L…労働力
- K…資本
- w…賃金
- r…レンタル料
グラフの描き方と費用最小化について解説しましょう。
等費用線を式で表す
C(費用)を式で表すと
C=wL+rKです。
労働者に対しては賃金を、機械が導入される場合はレンタル料を支払います。
両者のコストの合計がC(費用)です。
この公式さえ理解すれば、簡単に式を変形できます。K=の式に形を変えましょう。
まずは、各要素を移項してください。
rK=−C+wLとなりました。
rを両辺に割り算すると、と求められます。
この式を用いて、実際に等費用線を描いてみましょう。
関数は縦軸にK、横軸にLと置いています。
からK軸に接するのは切片の
です。
等費用線の傾きは、の絶対値が該当します。図に表したものがこちらです。
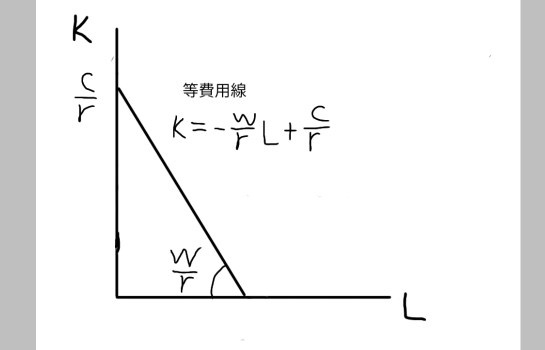
複雑に思えますが、内容は中学校の数学と大差ありません。
アルバイトの様子でも良いので、会社で働く環境と上手く連想させると分かりやすいです。

式はゴチャゴチャしているけど、1次関数と一緒か!

そう!グラフ自体は複雑ではないよ。
費用最小化=等量曲線の接点
すでに説明しましたが、企業が生産活動をするうえで重要なのは、いかに費用を抑えるかです。
最も費用が安くなるように労働と資本の量を調整します。
ここで使われるものが、上述した等量曲線です。
等費用線と等量曲線の接点が、費用を最も小さくさせる部分になります。
接点は費用最小化と呼ばれるため押さえておきましょう。
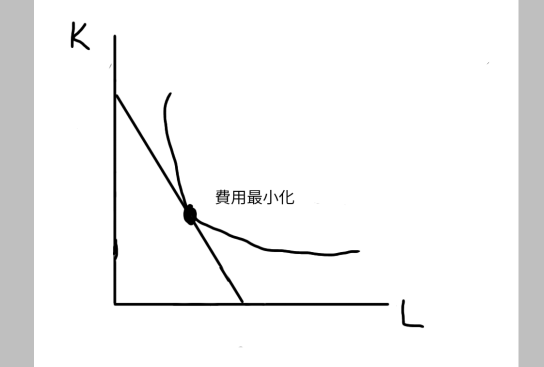
費用最小化は、等費用線と等量曲線の傾きが等しくなるポイントでもあります。
等量曲線の傾きは、技術限界代替率でした。
とも書き換えられます。
この値と生産要素の価格比であるが等しくなります。
つまり、費用最小化では以下の法則が成り立つと覚えましょう。
=
等量曲線と無差別曲線
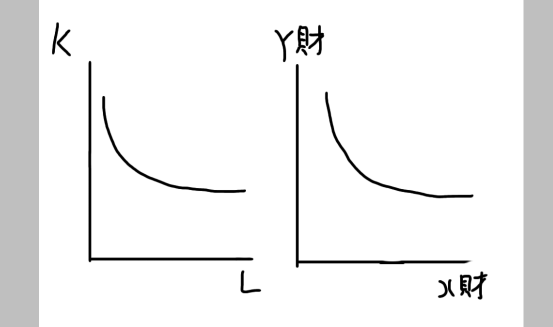
等量曲線と無差別曲線は、似た性質を持つと説明しました。
無論、概念は全く異なりますが、グラフの描き方はよく類似しています。
ただし、それぞれのグラフには次の相違点があると押さえてください。
- 等量曲線は具体的
- 無差別曲線は抽象的
等量曲線の場合は、資本や労働にどの程度投入するかを具体的に示します。明確に数値化し、戦略を立てられるのが特徴です。
一方で、無差別曲線は2つの財を見比べたときの満足度を測る指標でしかありません。
満足度を明確な数字に表すのは極めて難しく、あくまで抽象的なグラフです。
このような特徴を知っておけば、両者の立場(生産者と消費者)から経済を理解できます。

商品を買って満足かどうかは「主観」だもんね!

一方で企業側は正確なデータをもとに労働と資本を決めないといけない。
だから具体的なグラフを描けるんだ!
まとめ
今回は、等量曲線と等費用線について見ていきました。
資本と労働の配分を知る際には、等量曲線が使われます。加えて、等費用線も使うと費用最小化が分かります。
ここで触れた重要な部分をまとめたいと思います。
- 等量曲線の傾きが技術的限界代替率
- 費用最小化において等量曲線と等費用線の「傾き」が等しくなる
- 等量曲線は具体的、無差別曲線は抽象的
しっかりとおさらいし、等量曲線と等費用線を具体的にイメージできるよう頑張りましょう。