複数の企業が戦略を練るとき、互いに与える影響を考慮した上で意思決定するモデルがゲーム理論です。
以前はゲーム理論の中でも、ナッシュ均衡や囚人のジレンマについて解説しました。重要な内容なので以下のリンクも参考にしてください。
今回解説する内容は、同じくゲーム理論よりマックスミニ戦略(マキシミン戦略)です。これらは解き方がナッシュ均衡と異なります。
マックスミニ戦略が採られる意図と解き方の手順を押さえましょう。
マックスミニ戦略とは

マックスミニ戦略(マキシミン戦略)とは、はじめに各戦略の最小値を取り、その中から最大のものを選ぶ戦略のことです。
実際のビジネスのバトルでもそうですが、競合する相手がどういった戦略を取るかは分かりません。
そのため、自社にとって最も悪い状態のケースを最初に想定しようと考える企業もあります。
言い換えれば、考えうる最大の被害を最小に抑えられるかを目指す考え方です。
とはいえ、公務員試験のゲーム理論では定義についてはあまり問われません。表を使った問題が解けるように練習しましょう。

友達の車傷つけたのバレたらどうしよう
絶交?弁償?怒られるだけ?
何とか怒られるだけにしたい!!

いや、正直に話して謝ろうよ・・・
マックスミニ戦略の解き方
さっそく、マックスミニ戦略を使った解き方について紹介します。解き方は、上述で説明した定義を実際に試すだけです。
マックスミニ戦略の定義を手順として整理しましょう。
- 1.はじめに各戦略の最小値を取る
- 2.その中から最大のものを選ぶ
手順にしっかりと従えば、実際の問題もそこまで難しくはありません。
企業Aの戦略を分析
マックスミニ戦略について、以下の問題を作ってみました。以下の表を参考に、各プレイヤーがどの戦略を採るべきかを考えてみましょう。
なお、表では企業Aと企業Bの「利得」が記載されています。
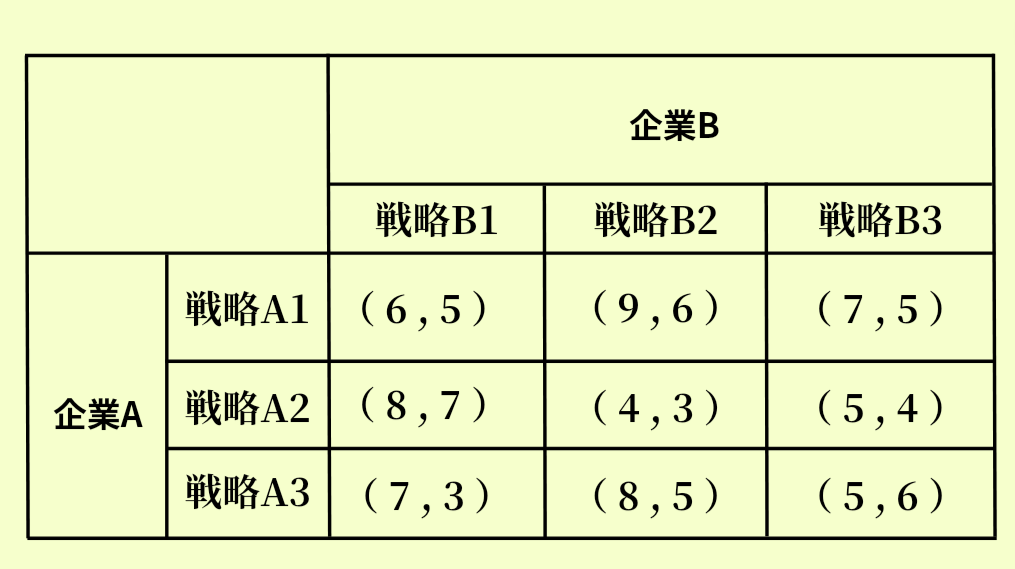
1番目の手順に従って各戦略の中から最小値を選びます。まずは、企業Aからチェックします。
企業Aが戦略A1を選んだとき、企業Bから見て最も数値が小さくなるものを選んでください。なお企業Aの数値は()内の左側が該当します。
企業Bの戦略と照らし合わせてみると次のようになります。
- 企業Bが戦略B1を選ぶ→6
- 企業Bが戦略B2を選ぶ→9
- 企業Bが戦略B3を選ぶ→7
この中で、最も数値が低くなるのは企業が戦略B1(数値は6)を選ぶときです。同じ理屈で他の戦略もチェックしてみましょう。
すると戦略A2の最小値は4、戦略A3の最小値は5であることが分かります。一度、情報を以下のように整理すれば解きやすいです。
- 戦略A1の最小値は6
- 戦略A2の最小値は4
- 戦略A3の最小値は5
この中から、最大の数値を選んでください。結果的に戦略A1が最も数値が大きく、被害がより少なくなると判断できるはずです。
企業Bの戦略を分析
同じ要領で企業Bの戦略を分析します。企業Bは、()内の右側の数字を見てください。
まずは、戦略B1の中から最も小さい値を選びましょう。右側の数字を見れば、企業Aが戦略A3を選んだときの「3」が該当します。
あとは同じ解き方で戦略B2と戦略B3の値を捉えるだけです。その結果、以下のように情報がまとまります。
- 戦略B1の最小値は3
- 戦略B2の最小値は3
- 戦略B3の最小値は4
この中で、最も値が大きいのは企業Bが戦略B3を選んだときです。
つまり、マックスミニ戦略に従うと企業Aは戦略A1を、企業Bは戦略B3を選択します。
マックスミニ戦略の応用
ここで、マックスミニ戦略の応用問題を紹介しましょう。以下の図を見てみてください。
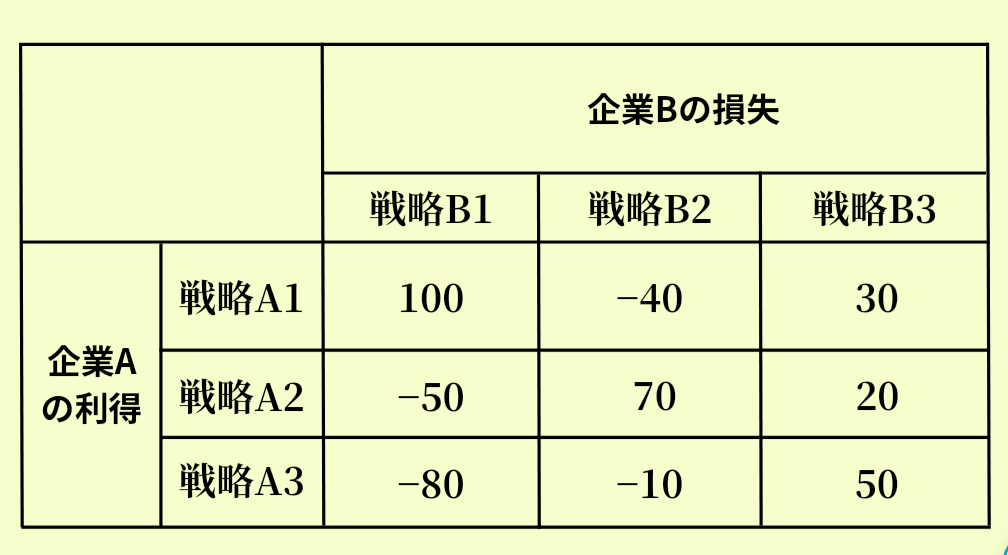
今度は()が書かれておらず、数字だけが書かれています。図にもあるとおり企業Aは利得を指しているものの、企業Bは損失を表す点もチェックしたいポイントです。
以上の条件を踏まえ、マックスミニ戦略の問題を解いてみましょう。
表の見方に注意する
上でも簡単に触れましたが、この場合は表の見方にも注意しなければなりません。企業Aは利得を示しているものの、企業Bの場合は損失と捉えます。つまり、先程の問題と異なる考え方が求められます。
企業Aの場合は、先程の問題と考え方自体は変わりません。具体的には後述しますが、各戦略の低い数字を選び、その中から最も高い数値を求めるだけです。
一方で、企業Bでは求める際に1つ作業する必要があります。その作業とは、全ての数字に「ー(マイナス)」をかけ算することです。
例えば、左上の数字は企業Bの損失が「100」の状態を指しています。100の損失を言い換えれば、利得が「−100」となっている状態です。理屈を押さえれば、理解しやすくなると思います。
企業Aの戦略を求める
解き方の手順を押さえたら、まずは企業Aのマックスミニ戦略を求めます。基本的に先程の問題と解き方は同じです。各戦略の最小値を求めましょう。すると以下のようにまとめられます。
- 戦略A1の最小値は−40
- 戦略A2の最小値は−50
- 戦略A3の最小値は-80
これらの最小値の中で、最も数値が高いのは戦略A1の「−40」です。つまり、企業Aは戦略A1を選びます。
企業Bの戦略を求める
次に、企業Bの戦略を求めます。しかし、この表で示されているのは損失です。そこで、各数値に「−」をかけ算して最小値を求めます。図にまとめると以下のとおりです。
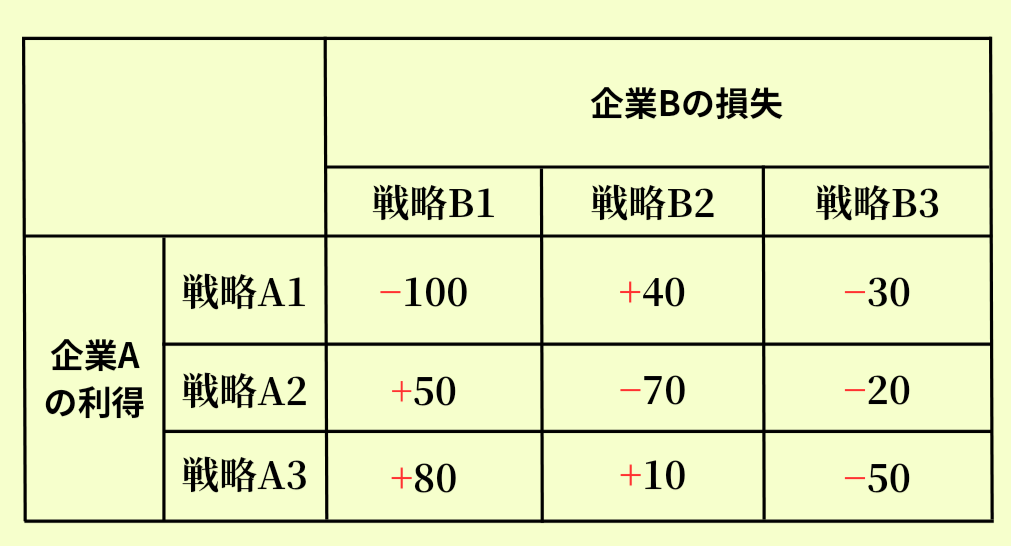
あとは、企業Aと同様に戦略B1〜戦略B3の最小値を求めてください。箇条書きでまとめると以下のようになります。
- 戦略B1の最小値は−100
- 戦略B2の最小値は−70
- 戦略B3の最小値は−50
これらの最小値の中で、最も数値が大きいのは戦略B3の−50です。
以上から企業Aは戦略A1、企業Bは戦略B3を選びます。
まとめ

今回は、ゲーム理論のマックスミニ戦略の解き方について解説しました。
- 1.はじめに各戦略の最小値を取る
- 2.その中から最大のものを選ぶ
以上の手順さえ押さえれば、実際に問題で出されてもスムーズに解けます。
練習問題を繰り返しながら、マックスミニ戦略を確実に正答できるようにしましょう。