公務員試験のミクロ経済学では、期待効用仮説の範囲も出題されます。
ただし、この範囲は非常に難問です。
計算も面倒なパターンが多く、しっかりと表を作成して解かなければなりません。ここでは、期待効用仮説の解き方をわかりやすく解説します。
手順をマスターし、出題されても正答に導けるよう準備しましょう。
期待効用仮説とは?
期待効用仮説は、不確実な世界を分析する際に使われる考え方です。
ただし定義が難しいため、具体例を用いながらわかりやすく解説します。
期待効用仮説の具体例
期待効用仮説が使われるケースは、宝くじや保険の購入です。ここでは、宝くじの例から説明しようと思います。
皆さんの中にも、一度は宝くじを購入したことがある方もいるでしょう。万が一、1等を当てると数億円と夢みたいな金額が貰えます。
ただし、実際に当たる確率は極端に低く設定されています。たいていの場合は、全く利益が得られないまま代金分を失うでしょう。
これらのバランスを考え、本当に宝くじを買った方がいいかを判断する考え方が期待効用仮説です。
期待効用仮説の計算方法
つづいて、期待効用仮説の計算方法もわかりやすく解説します。個人的には、ミクロ経済学の中でも最も計算が複雑だと思っています。
人によって捉え方が異なるとは思いますが、しっかりと対応できるように解き方を押さえてください。
期待効用を求める式は、
「確率×効用」です。
数学が好きな方はわかると思いますが、確率は一般的に分数や小数が使われます。
つまり問題文から効用を求め、確率を乗じて期待効用を導き出す流れです。
期待効用仮説の例題

期待効用仮説の例題を紹介します。ここでは基本的なやり方を学ぶべく、問題も簡単なものを用意しました。
本番では「√(ルート)」を使った問題も出てくるため、ケアレスミスはしないよう慎重に解きましょう。
期待効用の計算方法を押さえる
次に期待効用の計算方法を押さえましょう。問題に出てくる効用関数も参考にしてください。
まずは、宝くじが当たった場合の期待効用を求めます。20%の確率で、所持金は倍の1万円になります。
「+1万円」ではなく、「1万円になる」ですので問題文を読み間違えないでくださいね。
効用関数も書かれているため、代入しながら当てはめてみましょう。

代入すると、効用関数は「U=10,000」になります。
ここから、期待効用について求めてみましょう。
確率が20%、つまり0.2です。期待効用は「0.2×10,000」で2,000と出せました。
外れるパターンも計算する
今回の問題に出した宝くじでは、外れる確率が80%です。当たるパターンと同様に期待効用を求めてみましょう。

宝くじが外れたら、全額使った方の所得は「(5,000-r)」円です。効用も(5,000-r)で期待効用が(4,000-0.8r)となりました。
条件を元に表を記入する
期待効用仮説の問題では、下記の条件をまとめることがおすすめです。
- 所得
- 効用
- 確率
- 期待効用
これらの数値は、問題で書かれているパターンもあればわからない場合もあります。
数値がわからなければ、とりあえずは文字(xなど)で表してください。条件がある程度わかったら、下記のような表にしてまとめます。
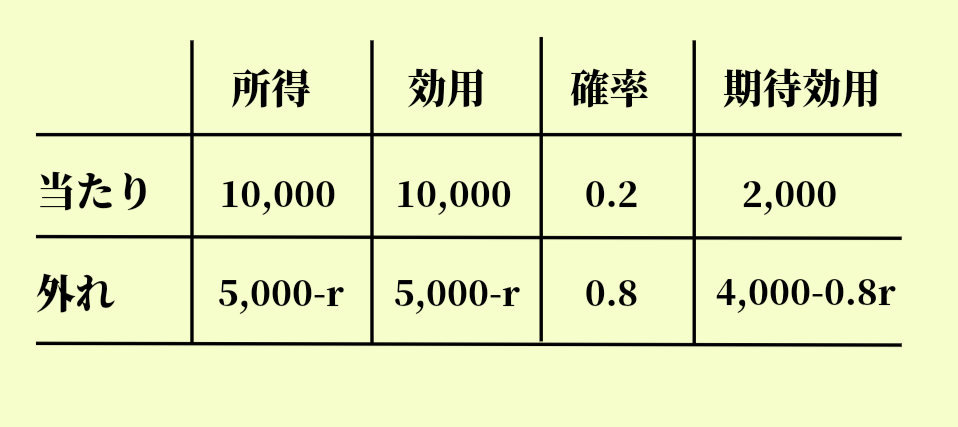
面倒だと感じるかもしれませんが、ケアレスミスを防ぐのに役立ちます。期待効用については、次の章を参考にしてください。
いくらなら購入するか求める
最後に、宝くじの値段がいくらまでなら購入するかを求めます。
当たるときの期待効用は2000でした。一方で、外れたときは(4000-0.8r)です。
まずは、それぞれを足しましょう。すると、「6000-0.8r」と表せます。
ちなみに、宝くじを購入しなければ所持金の「5000円」はそのままです。
つまり、「6000-0.8r」が「5000円」よりも大きくなればAさんは投資を行います。
この関係を式に表すと
「6000-0.8r≧5000」です。
こちらを計算すれば、
「r≦1250」と求められます。
後は数式を用いて「r」の値を求めます。答えは、1,250円です。
つまり、この方は宝くじの値段が1,250円までなら購入しようと考えます。
計算式を用いて人の購入意欲がわかるのは面白いですよね。
危険回避型の危険愛好型
では、最後に危険回避型と危険愛好型の話をします。
期待効用仮説では、これらの語句を押さえるとよりわかりやすくなるかと思います。それぞれの簡単な説明は次のとおりです。
- 危険回避型…堅実な人
- 危険愛好型…冒険したい人
詳しく内容を説明しましょう。
危険回避型は堅実な人
危険回避型とは、ギャンブルをあまり好まない堅実な人です。筆者はどちらかというと、こちらの部類に該当します。
危険回避型の場合、効用関数の指数が分数(小数、もしくは指数ではなく√を使う)になると覚えてください。
例えば、50%の所得が100になるとします。一体、この人はどのくらい支払うかを求める問題です。
効用関数と期待効用を求める式は以下の図のとおりです。

このように、危険回避型の場合は宝くじや保険を慎重に購入します。
危険愛好型はギャンブル好き
反対に、危険愛好型の場合はギャンブル好きが該当します。効用関数の特徴は、指数が整数になることです。
ちなみに、指数がない人は危険中立型とされています。ギャンブルを避けようとは思わないものの、特に好きでもない人です。
先程の条件を使って、危険愛好型の期待効用も求めてみましょう。

このように危険愛好型は、危険回避型よりも期待効用が大きくなります。
まとめ
今回は、期待効用仮説の解き方をわかりやすく解説しました。
ミクロ経済学の中でも、比較的計算方法が複雑なパターンのひとつです。まずは、「期待効用=確率×効用」の式を押さえましょう。
- 期待効用
- 確率
- 効用
上記のそれぞれの数値について、表を用いながら求めます。加えて、危険回避型と危険愛好型の語句の意味は覚えてください。
この問題が解けるようになれば、ミクロ経済学の大体の問題は制覇できると思います!