今回もマクロ経済学について記事を書いてみようと思います。
本日の内容は『産業連関表』です。
産業連関表は、一体どのようなものなのかをここで確実に押さえるようにしましょう。公務員試験を受験される方は、マクロ経済学の勉強で使うのでぜひ参考にしてください。
・投入係数表の見方を押さえる
産業連関表とは
産業連関表とは、ある産業の生産と販売の様子をマトリックスにした指標です。何を表しているか分かりづらいと思うので、もう少し噛み砕いて説明しましょう。
産業は基本的に何か商品を生産する一方で、それを販売してお金を稼ぐ方法を指します。
この活動の一環を「行」と「列」にまとめたものが産業連関表です。
Excelでいう行は「横のセル」、列は「縦のセル」を指します。
今回、産業連関表のサンプルを作ってみました。
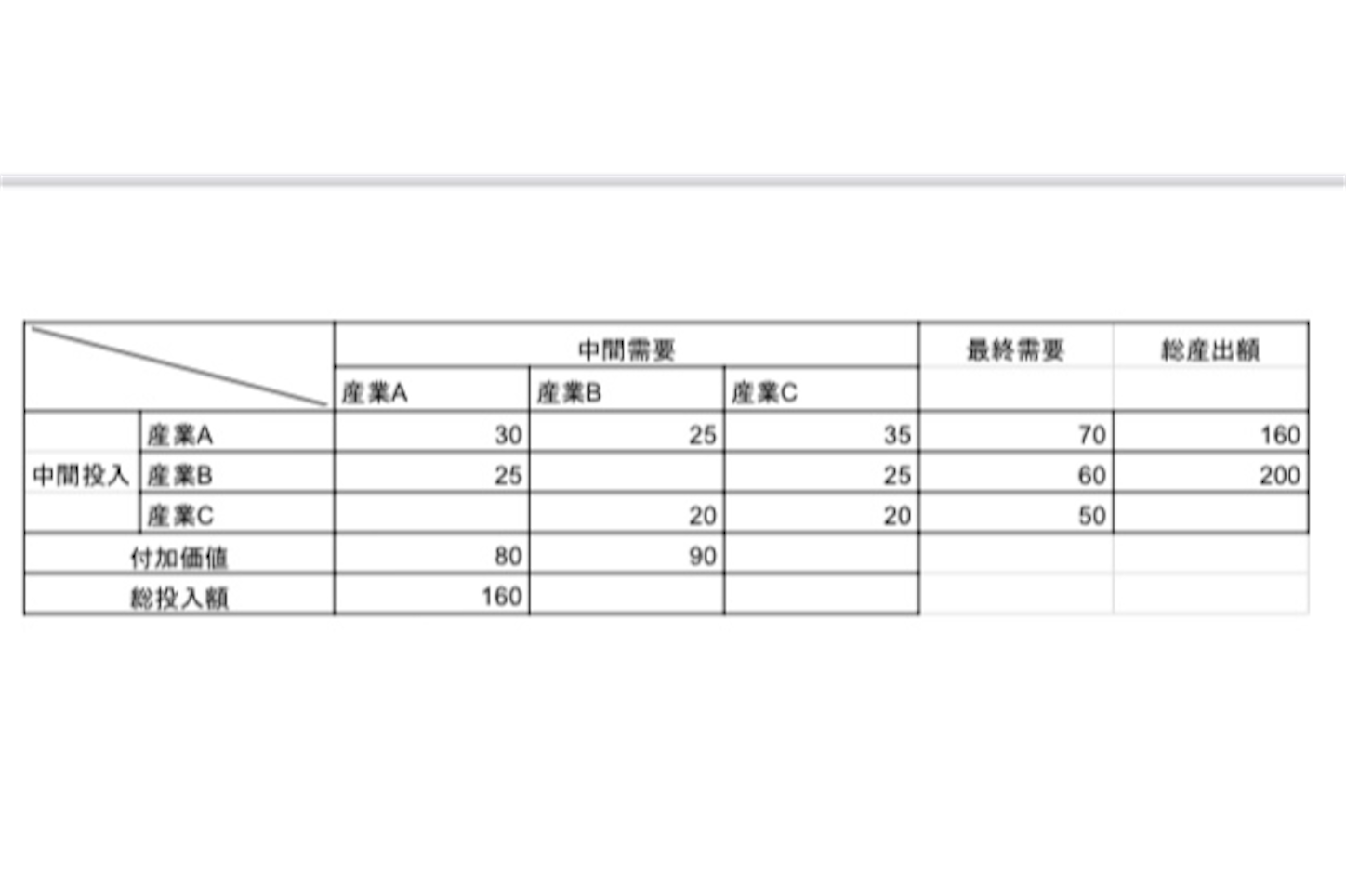
産業連関表の「行」は基本産出構造を表します。反対に「列」は投入構造を表すものです。
この指標を上手く使うことで最終的には国内総生産(GDP)が求められます。
産業連関表の使い方
では、産業連関表を使って具体的な数値等を求めていきましょう。
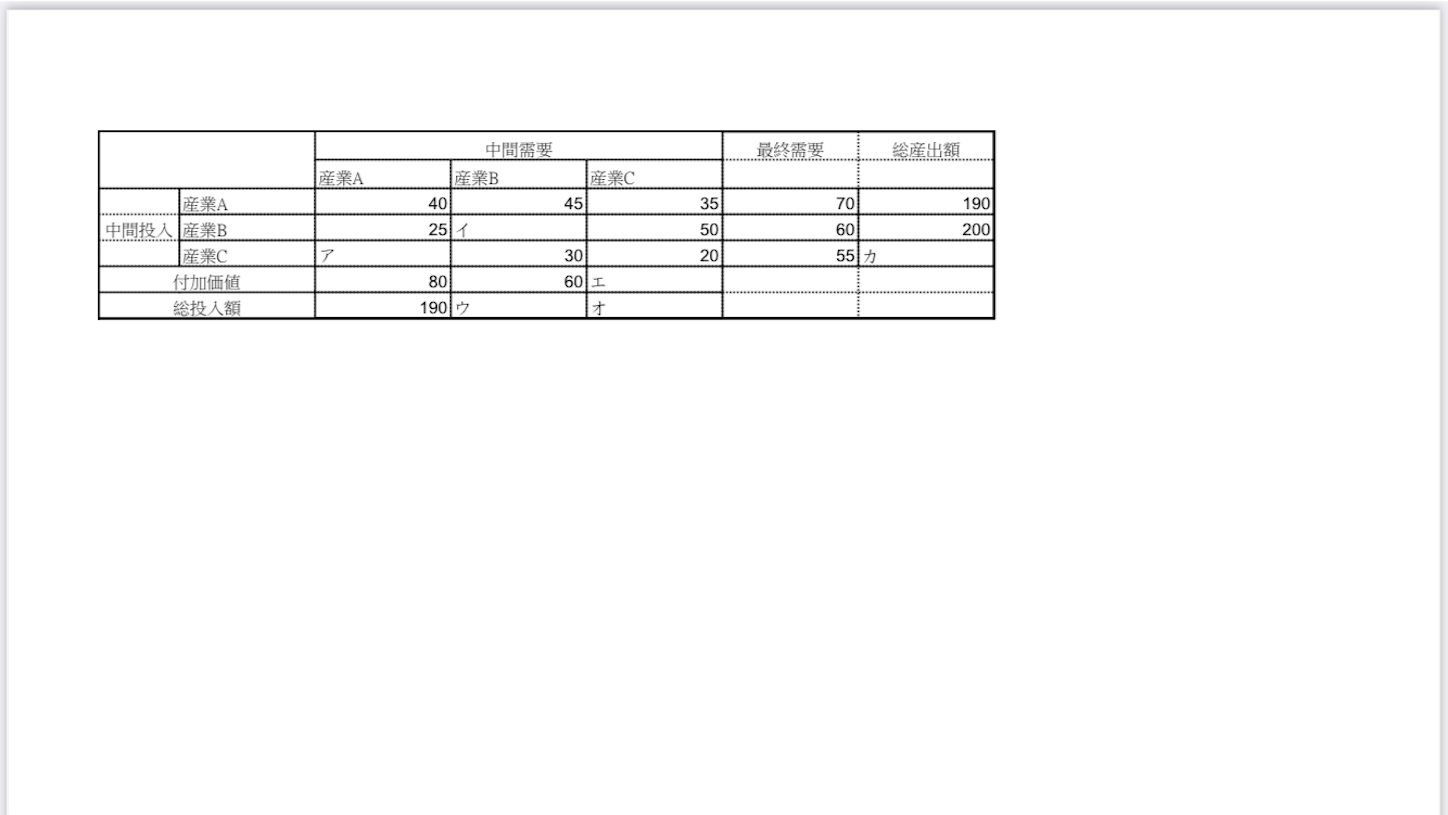
図を見てもらうと分かりますが、列(縦)で数値を確認します。
産業Aが上から
40、25、(ア)、80、190
産業Bが上から
45、(イ)、30、60、(ウ)
産業Cが上から
35、50、20、(エ)、(オ)です。
最終需要は上から70、60、55です。
この状況から「空白部分に入る数値」を求めましょう。
はじめに絶対押さえてほしいのが、総投入額と総産出額の数値は絶対に等しくなることです。
総投入額または総産出額の片方だけが空白になっている場合は、。
まず、(ウ)は200になります。
総投入額(総産出額)の求め方は「産業A+産業B+産業C+最終需要」です。
つまり、それぞれの産業の数値を求めるためには総投入額(総産出額)からそれぞれの数値を引き算していけば空白部分が求められます。
(ア)は
(ア)=190−(40+25+80)
(ア)=45となります。
すでに(ウ)が求められているので(イ)も答えを出せますね。
(イ)=200−(45+30+60)
(イ)=65です。
(ア)の数値が出ているので(カ)はすぐに答えが出てきます。
(カ)=45+30+20+55
(カ)=150ですね。
するとそのまま(オ)も数値が出ます。
(オ)=150となりますね。
そうすれば(エ)が
(エ)=150−(35+50+20)
(エ)=45と求められました!
【答え】
(ア)=45
(イ)=65
(ウ)=200
(エ)=45
(オ)=150
(カ)=150
ちなみに、付加価値と最終需要の合計はGDPの三面等価の原則より同じ数値となります。
最終需要の総額は
『70+60+55=185』
付加価値に当てはまると
『(エ)=185−(80+60)』
『(エ)=45』
と求める方法でもOKです。
練習問題
続いては先程の例を生かして練習問題を解いていきましょう。
産業連関表はこちらです。
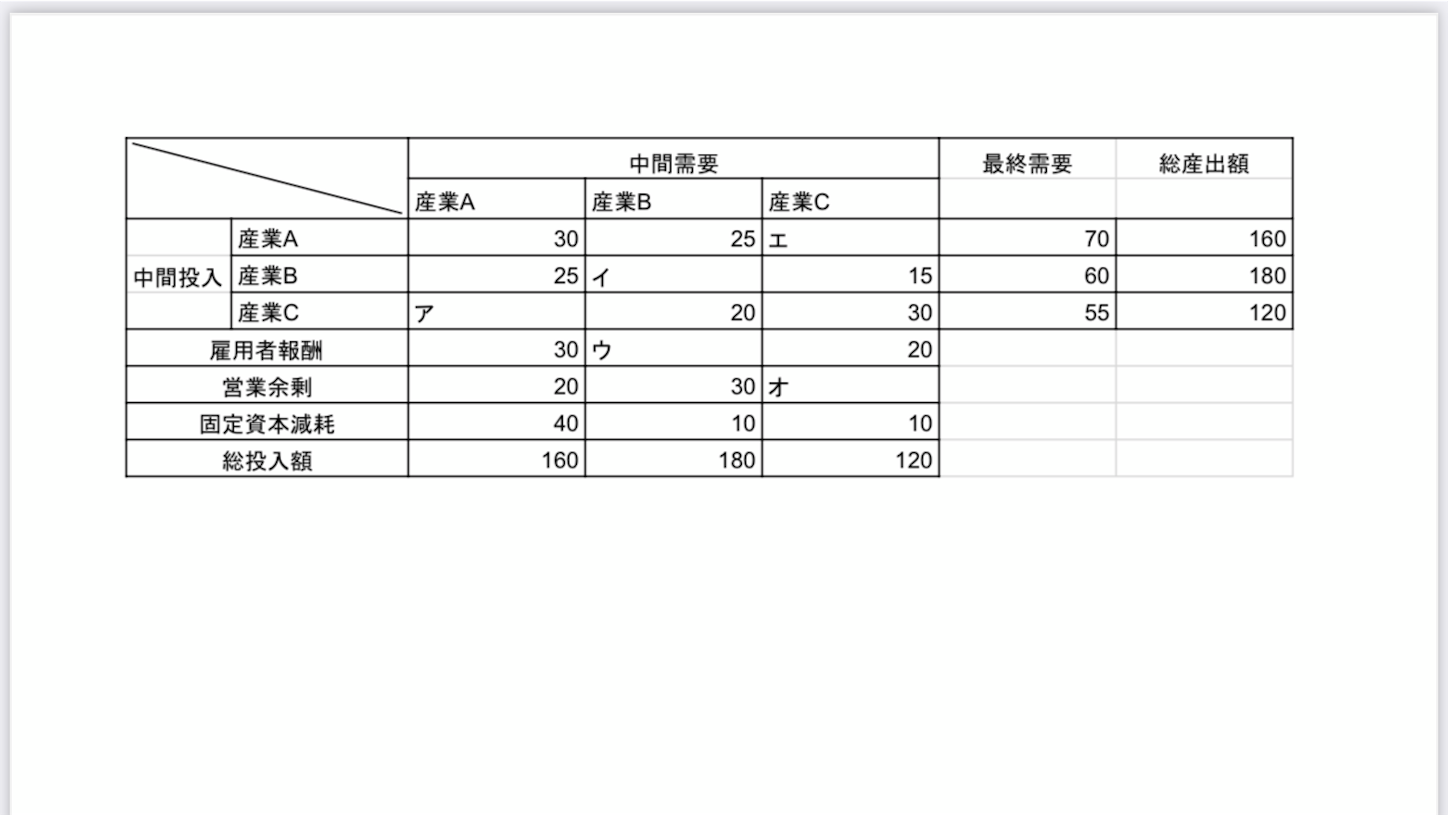
最初に言っておきますが、これから出題する問題は前半部分なら例題の応用で解けますが、後半部分が難しいかもしれません。
「この産業連関表の空白部分とGDPを求めよ。
(ただし、間接税と補助金は考慮しない)」
ルーズリーフやチラシの裏でもいいので、計算しながら解いてみてください。
空白部分を求める方法
計算する際には、以下の2点を意識することが大切です。
- 総投入額と総産出額を合わせる
- 総投入額(総産出額)から数値をどんどん引く
この問題も計算していけば簡単に求められるよう設定しました!
『(ア)=160−(30+25+30+20+40)』
『(ア)=15』
『(イ)=180−(25+15+60)』
『(イ)=80』
『(ウ)=180−(25+80+20+30+10)』
『(ウ)=15』
『(エ)=160−(30+25+70)』
『(エ)=35』
『(オ)=120−(35+15+30+20+10)』
『(オ)=10』です。
GDPを求める方法
続いて『GDP』の求め方を書きましょう。
数値だらけなので何を使えばいいか迷ったかもしれません。
しかし、GDPの計算式で見慣れた言葉が出てきていますよね?
『雇用者報酬、営業余剰、固定資本減耗』です。
これらは分配面の視点からGDPを求めるときに利用しましたね。
GDPの計算で使う数値は上に挙げたものだけです。残りの数値は無視してください。
すると、以下の3つの式が完成します。
- 30+20+40=90
- 15+30+10=55
- 20+10+10=40
【答え】
(ア)=15
(イ)=80
(ウ)=15
(エ)=30
(オ)=10
GDP=185
投入係数
最後に『投入係数』も説明しましょう。
まずは、この表を見てください。(見づらいのは申し訳ないです。)

0.4、0.1、0.3、0.2と小数がありますね。
これらが投入係数であり、この数値を使った表は投入係数表と言われます。
1つの生産に対してどの程度の原材料を使ったか指し示すものです。
例えば、パン1個作るのにどの程度の小麦や機械の燃料を使ったのかを表した数値ですね。
『各々の投入額÷総産出額』で投入係数は求められます。
この式を入れ替えれば
『投入額=総産出額✕投入係数』となります。
つまり、『ア、イ、ウ、エ』はそれぞれ
『ア=200✕0.4』
『イ=200✕0.1』
『ウ=100✕0.3』
『エ=100✕0.2』
となり
『ア=80』
『イ=20』
『ウ=30』
『エ=20』
が答えです。
産業連関表の要点整理
今回は公務員試験のマクロ経済学より、産業連関表の求め方について解説しました。
産業連関表の問題が出題されたら、まずは以下のポイントを意識してください。
- 総投入額と総産出額の数値は同じ
- 付加価値と最終需要の計が等しくなる
- 全ての産業の数値+付加価値(最終需要)=総投入額(総産出額)
投入係数に関しては、以下の計算方法を押さえましょう。
- 各々の投入額÷総産出額=投入係数
- 総産出額✕投入係数=各々の投入額
数字がいろいろと出てきますが、落ち着いて計算することが大切です。