どーも、ヤマトノです。
前回もマクロ経済学からGDPデフレーターについて解説しました。
ここから計算問題が続きます。
今回は「均衡国民所得」について触れていきましょう。マクロ経済学の基本であるため、確実に得点できるよう押さえてください。
均衡国民所得とは?
まずは、均衡国民所得の用語の説明をしましょう。
世の中の経済は常に
- 需要
- 供給
で成り立っています。
例えば、お腹が空いたら我々はコンビニやスーパーでお弁当を買ったり、レストランやラーメン屋さんでご飯を食べたりするはずです。
これは、食べ物を欲するための行動であり、経済用語では「需要」と言われています。人々の需要に答えるべく、各店舗で食べ物を販売する行為が「供給」です。
中学校や高校の頃に、財と価格を座標にして需要曲線と供給曲線から均衡価格を求めるグラフを書いた経験はありませんか?

主に均衡価格はミクロ経済学の話になりますが、今回勉強する均衡国民所得は同じような理論に基づいて求められるのです。
45度分析と呼ばれる手法で、X軸に国民所得・Y軸に需要・供給を置くと下記のようなグラフが出来上がります。
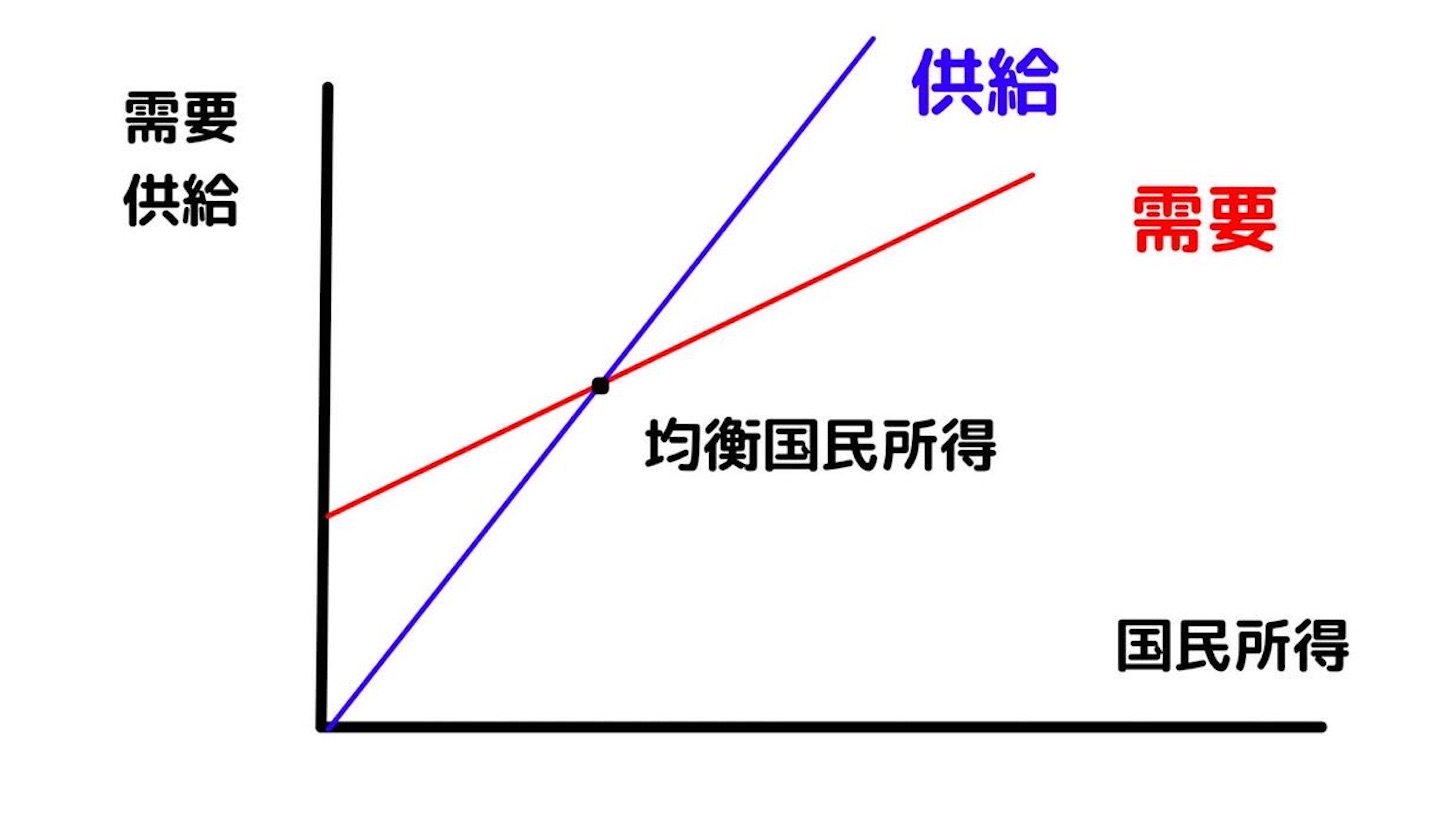
需要曲線と供給曲線のぶつかっているところが均衡国民所得に当たるため、殆どミクロ経済学の均衡価格と同じ要領ですね。
マクロ経済学は国全体の経済現象から研究する学問であるため、国民所得と大きいカテゴリーで需要・供給の関係を捉えています。
つまり、均衡国民所得は国全体の需要と供給の値が一致する時点での所得水準です。
均衡国民所得の状態では、インフレーションやデフレーションによるギャップもありません。
均衡国民所得の計算方法

均衡国民所得の計算では下記の公式を絶対に押さえてください。
Y=C+I+G
マクロ経済学において、何度も使用される式です。
公務員試験でも、均衡国民所得の公式にさまざまな数値を求める計算問題が出題されます。
左辺から順番に、Yは国民所得を表すアルファベットです。
国民所得を求めるためには、民間消費(C)・民間投資(I)・政府支出(G)を全て合わせます。
所得を算出する計算では、三面等価の原則から支出面でも求められるルールがありました。下記の記事から参考にしてください。
均衡国民所得の計算問題
では、実際に問題を解いてみましょう。
既に解いた方やどうしても分からない方は、下記の説明を参考にしてください。
まずは、「C(民家消費)」の値を整理していきましょう。(やり方はいろいろあるので1つの例です。)
民間消費の値は
C=0.4(Y-T)+20
でした。
T(租税)の値は0.5Yと定められているので、Cの式に代入していきます。
すると、
C=0.4(Y-0.5Y)+20となり、
C=0.4×0.5Y+20
C=0.2Y+20と整理できました。
I=40、G=20もそれぞれ代入して
Y=0.2Y+20+40+20
0.8Y=80
8Y=800
Y=100
答えは3番です
応用問題にチャレンジ
続いて、問題の難易度を上げてみます。
今回は√の中にYが入っており、問題自体が複雑となっています。
ただ、基本的な計算方法は変わらないので一通り解いていきましょう。
まず、Cの値だけ先に求めると
C=0.5(Y-0.2Y)
C=0.4Y
次に国民所得の値を出します。
Y=0.4Y+6√Y+720
方程式を使って求めます。
移行すると
Y-0.4Y-6√Y-720=0
0.6Y-6√Y-720=0
6Y-60√Y-7200=0
Y-10√Y-1200=0
さて、Yの値を求めたいのですが、√が邪魔で上手くまとめられません。
しかし、少し捻って考えれば実は簡単に整理できるのです。
√が邪魔なのであれば、無駄に外そうと考えずに、そのまま因数分解すれば意外とスムーズにYの値が出てきます。
例えば、「2」を√で表すと
「」と書き換えられますよね。(√2の二乗)
つまり、Yも同様に「」と直せば簡単です。
すると、−
−
=
(√Y-40)(√Y+30)=0
と求まりました。
二次方程式を解くと√Y=40,-30となります。
負の値はふさわしくないため、
√Y=40
を用います。
後は2乗するだけです。
Y=1600
答えは1600と求められました。(2番が正解)
まとめ
マクロ経済学も計算問題が続きます。
均衡国民所得の公式や計算に関しては、どういった問題が出題されても答えられるようにしましょう。
今回の応用問題は、国家総合職や裁判所職員の試験を受ける場合に出題される傾向があります。
計算を上手く解けるかが、マクロ経済学を得点源にするコツです。